Этот вид статистических гипотез относится к гипотезам о виде закона распределения генераль­ной совокупности.

Сформулируем нулевую и конкурирующую ги­потезы согласно условию задачи.

Н ₀: X ~ R (кч) — случайная величина X подчи­няется равномерному распределению с параметра­ми (к;ч).

Н ₁ случайная величина X не подчиняется рав­номерному распределению, числа неудачных результатов неслучайно.

В качестве критерия для проверки статистичес­ких гипотез о неизвестном законе распределения генеральной совокупности используется случайная величина χ ². Этот критерий называют критерием Пирсона.

Его наблюдаемое значение (χ ²_наб.) рассчитывает­ся по формуле

где т _эi — эмпирическая частота i - йгруппы вы­борки;

т _mi — теоретическая частота i - й группы выборки.

Составим таблицу распределения эмпирических
и теоретических частот (табл. 2).

Таблица 2

т эi
т mi

Найдем наблюдаемое значение χ ²_наб.

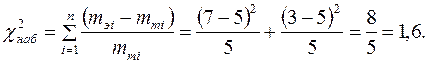
Критическое значение (χ ²_кр.) следует определять с помощью таблиц распределения χ ²(приложение) по уровню значимости α и числу степеней свободы k.

По условию α = 0,05, а число степеней свободы рассчитывается по формуле

K = n – l -1,

где k — число степеней свободы; п — число групп выборки; l — число неизвестных параметров пред­полагаемой модели, оцениваемых по данным вы­борки (если все параметры предполагаемого закона известны точно, то l = 0).

По условию задачи, число групп выборки (п)рав­но 2, так как могут быть только 2 варианта результатов игры: «удачные» и «неудач­ные», а число неизвестных параметров равномер­ного распределения (l)равно 0.

Отсюда k = 2-0 - 1 = 1.

Найдем χ ²_кр. по уровню значимости α = 0,05 и числу степеней свободы k = 1:

χ ²_{кр.( α=0,05;к=1)} = 3,8.

χ ²_наб.< χ ²_кр. следовательно, на данном уровне зна­чимости нулевую гипотезу нельзя отклонить, расхождения эмпирических и теоретических час­тот — незначимые. Данные наблюдений согласуют­ся с гипотезой о равномерном распределении гене­ральной совокупности.

Это означает, что для утверждения о том, что действия крупье неслучайны, нет оснований и на уровне значимости α= 0,05 мож­но утверждать, что игра ведется честно.

Ответ. На уровне значимости α = 0,05 можно ут­верждать, что полученные результаты игры не позволяютсделать вывод о нечестной игре со стороны крупье.

Пример 6. На уровне значимости α = 0,025 про­верить гипотезу о нормальном распределении гене­ральной совокупности, если известны эмпиричес­кие и теоретические частоты (табл. 3):

Таблица 3

т эi
т mi

Решение. Сформулируем нулевую и конкуриру­ющую гипотезы согласно условию задачи.

H ₀: X~N (a; σ ²) — случайная величина X подчи­няется нормальному закону распределения с пара­метрами а и σ².

Н ₁:случайная величина X не подчиняется нор­мальному закону распределения с параметрами а и σ².

В качестве критерия для проверки нулевой ги­потезы используем критерий Пирсона χ ².

Найдем наблюдаемое значение χ ²_наб.:

Найдем критическое значение критерия (χ ²_кр.) по таблице распределения χ ² (приложение)по уров­ню значимости α и числу степеней свободы k.

Дата добавления: 2015-07-10