Вывод сделайте самостоятельно и попытайтесь объяснить полученные результаты и в чем их отличие от примера 2.

Пример 4. Продукция одного вида хранится в 2-х складских помещениях, которые различаются по условиям хранения. Для оценки качества условий хранения через 1 год нахождения продукции в складских помещениях проведен ее выборочный контроль и получены результаты, представленные в табл.1.

Таблица 1

Выборки	Склад №1	Склад №2
Объем выборки	n 1=200	n 2=300
Число не исправных деталей	m 1=20	m 2=15

На уровне значимости α = 0,025 определите, име­ется ли существенное различие в качестве хранения продукции на складах?

Решение. Для решения данной задачи необходи­мо сравнить 2-е вероятности биномиальных распре­делений.

Сформулируем нулевую и конкурирующую ги­потезы согласно условию задачи.

Н ₀: р ₁ = р ₂ — вероятности появления события в 2-х генеральных совокупностях, имеющих биномиальное распределение, равны (применительно к ус­ловию данной задачи — вероятность того, что единица продукции, хранящейся на 1-м складе, окажется брако­ванной, равна вероятности того, что единица продукции, хранящейся на 2-м складе, окажется брако­ванной).

Н ₁: p ₁ ¹ р ₂ — вероятности появления события в 2 генеральных совокупностях, имеющих биномиаль­ное распределение, не равны (применительно к усло­вию этой задачи — на надежность продукции существенное влияние оказывают условия хранения). Так как по условию задачи не требуется проверить, на каком складе качество хранения лучше, выд­вигаем двустороннюю конкурирующую гипотезу.

Поскольку конкурирующая гипотеза — двусто­ронняя, то и критическая область — двусторонняя.

В качестве критерия для сравнения 2-х вероятно­стей биномиальных распределений используется случайная величина V.

Его наблюдаемое значение v _наб рассчитывается по формуле:

где m _l/ n ₁ — относительная частота (частость) появ­ления события в 1-й выборке;

m ₂/ п ₂ — относитель­ная частота (частость) появления события во 2-й выборке;

— средняя частость появления события;

— средняя частость непоявления события,

Так как конкурирующая гипотеза — двусторон­няя, критическое значение v _кр следует находить по таблице функции Лапласа из равенства

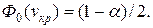
По условию α = 0,025.

Отсюда

Ф ₀ (v _кр)= (1 - 0,025)/2 = 0,4875.

По таблице функции Лапласа найдем, при каком и _кр Ф ₀ (и _кр)= 0,4875.

Ф₀(2,24) = 0,4875.

Учитывая, что конкурирующая гипотеза — дву­сторонняя, находим две, критические точки

v _крпр = 2,24; - v _крлев = - 2,24.

- v _кр< v _наб< v _кр, следовательно, наблюдаемое значение критерия попадает в об­ласть допустимых значений и на данном уров­не значимости нет оснований отвергнуть нулевую гипотезу. По имеющимся данным на уровне значи­мости α = 0,025 нет оснований отклонить нулевую гипотезу. Следовательно, условия хранения продукции на складах одного качества.

Ответ. Нет оснований отклонить нулевую гипо­тезу, т. е. имеющееся различие в качестве хранимой продукции на уровне значи­мости α = 0,025 случайно и незначимо.

Пример 5. При игре в рулетку игрок принимает условие ставить только на «красное» или «черное». В 7 случаях из 10 он проигрывает и подозревает, что крупье ведет нечестную игру. На уровне значимости 0,05 определи­те, случайны ли результаты игры?

Решение. Для того чтобы ответить на поставлен­ный вопрос, необходимо проверить статистическую гипотезу о том, совпадает ли данное эмпирическое распределение числа выигрышей (проигрышей) с равномерным теоретическим распределением?

Дата добавления: 2015-07-10