С. Распределение Фишера - Снедекора (F – распределение).

РаспределениемФишера – Снедекора называется распределение случайной величины

где χ ²(k ₁) и χ ²(k ₂) -случайные величины, имеющие χ ² - распределение соответственно с k ₁ и k ₂ степенями свободы.

Задание 1. Попытайтесь обосновать тот факт, что распределение χ ² положено в основу многих критериев проверки статистических гипотез.

Пример 1. Для контроля качества обучения в двух школах восьмых классов было проведено тестирование 32 учеников первой и 45 учеников второй школы: n _x =32; n _y = 45.

По результатам тестирования были подсчитаны средние баллы для тестируемых учеников первой и второй школы. Они соответственно оказались равными: 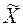= 4,45; =4,19.

До начала тестирования школы представили сведения, свидетельствующие о тот, что успеваемость учеников восьмых классов, оцениваемая средним баллом за год обучения находится для этих школ на одном и том же уровне . Однако дисперсия среднего балла для этих школ различная и соответственно имеет следующие значения: D (X)= 1,1; D (Y)= 1,61. Отклонения уровня успеваемости учащихся в каждом классе распределены по нормальному закону.

Требуется на уровне значимости α = 0,05 проверить, существенно ли по­лученное различие средних показателей успеваемости учащихся или эти различия не существенны.

Решение. Для решения данной задачи необходи­мо сравнить 2 средние величины из нормально распределенных генеральных совокупностей, дисперсии которых известны. В данной задаче речь идет о больших выборках, так как п _х = 32 и п _y =45 больше 30. Выборки — независимые, так как из контекста задачи видно, что они извлечены из непересекающихся генераль­ных совокупностей.

Сформулируем нулевую и конкурирующую ги­потезы согласно условию задачи.

Н ₀: = — генеральные средние двух нормально распределенных совокупностей с известными дис­персиями равны (применительно к условию данной задачи — учащиеся двух школ имеют на уровне значимости α = 0,05 одинаковую успеваемость).

Н ₁: — генеральные средние двух нормально распределенных совокупностей с известными дисперсиями не равны.

Конкурирующая ги­потеза двусторонняя, так как из условия задачи не следует, что необходимо выяснить больше или меньше успеваемость в одном из классов по сравнению с другим.

Поскольку конкурирующая гипотеза — двусто­ронняя, то и критическая область — двусторонняя.

В качестве критерия для сравнения 2-х средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки), исполь­зуется случайная величина Z.

Его наблюдаемое значение (Z _наб)рассчитывается по формуле:

(1)

где 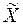— выборочная средняя для X;

— выбороч­ная средняя для Y;

D (X) — генеральная дисперсия для X;

D (Y) — генеральная дисперсия для Y.

Задание 2.Попытайтесь обосновать справедливость формулы (1).

Так как конкурирующая гипотеза — двусторон­няя, критическое значение (Z _кр) следует находить по таблице функции Лапласа (см. приложение)из ра­венства

.

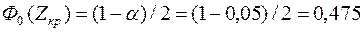Отсюда

Ф₀(1,96) = 0,475.

Учитывая, что конкурирующая гипотеза — дву­сторонняя, находим две критические точки:

Z _кр-п = 1,96; Z _кр-л = -1,96 (см. рис. 1).

Рис. 1. Область принятия решений

Заметим, что при левосторонней конкурирующей гипотезе Z_кр следует находить по табли­це функции Лапласа (приложение)из равенства Ф ₀(Z _кр) = (1 - 2 α)/2 и присваивать ему знак «минус».

При правосторонней конкурирующей гипотезе Z_кр находим по таблице функции Лапла­са (приложение)из равенства Ф ₀(Z _кр) = (1 - 2 α)/2.

В результате имеем, что Z_наб<Z_кр, следовательно, на данном уровне зна­чимости нулевая гипотеза не отвергается в пользу кон­курирующей. На уровне значимости α = 0,05 мож­но утверждать, что полученное различие средних показателей успеваемости в школах случайно, их уровень примерно одинаков (на уровне доверия равном γ = 1- α =0,95).

Наблюдаемое значение критерия попадает в кри­тическую область, следовательно, нуле­вая гипотеза отклоняется в пользу конкурирующей.

Ответ. На уровне значимости α = 0,05 можно ут­верждать, что полученное различие средних по­казателей тестирования учащихся в двух школах случайно, знания учащихся, контролируемые тестом, для обеих школ одинаковы.

Задание 3.В рамках условия примера 1, при = 4,45 определите при каком результате следует отвергнуть нулевую Н ₀ гипотезу и принять конкурирующую гипотезу Н ₁. Ответ. ₁ =3,93; ₂= 4,96.

Пример 2. Предлагаетсяновая методикаорганизации обслуживания

автомобилей, применение которой при том же объеме обслуживания сократит время на его проведение. Проведение обслуживания (ТО-1) 9 автомобилей по старой методике и 15 автомобилей - по новой методике дало сле­дующие результаты:

- среднее время обслуживания старым методом 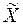= 60 мин, выборочная дисперсия s ²_x = 180 (мин²);

- среднее время обслуживания новым методом = 50 мин, а выборочная дисперсия s ²_y = 150 (мин²).

На уровне значимости α = 0,01 следует установить, позволило ли использование нового метода со­кратить время обслуживания автомобилей?

Решение. Для решения данной задачи необходи­мо сравнить 2 средние нормально распределенных генеральных совокупностей, генеральные диспер­сии которых неизвестны,но предполагаются оди­наковыми (малые независимые выборки). В этой задаче речь идет о малых выборках, так как п _х = 9и п _у = 15 меньше 30. Выборки — независимые, по­скольку из контекста задачи видно, что они извле­чены из непересекающихся генеральных совокуп­ностей.

Сформулируем нулевую и конкурирующую ги­потезы, согласно условию задачи.

Н ₀: = — генеральные средние двух нормально распределенных совокупностей с неизвестными дис­персиями (предполагаемыми одинаковыми) рав­ны, т.е. новая и старая методики по времени выполнения ТО-1 равнозначны.

Н ₁: > — генеральная средняя для X боль­ше, чем генеральная средняя для У, т.е. новая методики по времени выполнения ТО-1 дает выигрыш.

Так как конкурирующая гипотеза — правосторон­няя, то и критическая область — правосторонняя.

Приступать к проверке гипотезы о равенстве ге­неральных средних 2-х нормально распределенных совокупностей с неизвестными дисперсиями мож­но лишь в том случае, если генеральные дисперсии равны. В противном случае, данная задача теоретически неразрешима.

Поэтому, прежде чем проверять эту гипотезу, проверим гипотезу о равенстве генеральных диспер­сий нормальных совокупностей.

Сформулируем для этого дополнительного условия нулевую и конкурирующую ги­потезы, согласно условию задачи.

H ₀: D (X) = D (Y) — генеральные дисперсии 2 нор­мально распределенных совокупностей равны.

Н ₁: D (X) > D (Y) — генеральная дисперсия для X больше генеральной дисперсии для Y. Выдвигаем правостороннюю конкурирующую гипотезу, так как выборочная дисперсия для X значи­тельно больше, чем выборочная дис­персия для Y.

Так как конкурирующая гипотеза — правосторон­няя, то и критическая область — правосторонняя.

В качестве критерия для сравнения 2-х дисперсий нормальных генеральных совокупностей использу­ется случайная величина F — критерий Фишера-Снедекора (приложение).

Его наблюдаемое значение (f _наб) рассчитывается по формуле

где S _б — большая вы­борочная дисперсия;

S _м — меньшая выборочная дисперсия.

Критическое значение (f _кр)следует находится по таблице распределения Фишера-Снедекора (приложение)по уровню значимости α и числу степеней свободы k ₁ и k ₂.

По условию α = 0,01; число степеней свободы найдем по формуле

k ₁ = п _х – 1 = 9 – 1 = 8;

k ₂ = п _у – 1 = 15 – 1 = 14.

Определяем f _кр по уровню значимости α = 0,01 и числу степеней свободы k _l = 8 и k ₂ =14:

f _{кр(9;14; α = 0,01 )} = 4,14.

Имеем, что f _наб< f _кр,следовательно, на данном уровне зна­чимости нет оснований отвергнуть нулевую гипоте­зу о равенстве генеральных дисперсий нормальных совокупностей.

Следовательно, можно приступить к проверке гипотезы о равенстве генеральных средних двух нормально распределенных совокупностей.

В качестве критерия для проверки этой гипоте­зы используется случайная величина t -критерий Стьюдента. (Почему?)

Его наблюдаемое значение (t _нa6)рассчитывается по формуле

Критическое значение (t _кр)следует находить по таблице распределения Стьюдента (приложение)по уровню значимости α и числу степеней свободы k.

По условию α = 0,01; число степеней свободы найдем по формуле

k= п _х + п _у – 2 = 9 + 15 - 2 = 22.

Найдем t _кр по уровню значимости α = 0,01 и числу сте­пеней свободы k = 22 для односторонней критической области:

t _{кр(0,01; 22)} = 2,51.

Таким образом, имеем: t _нa6 < t _к или 1,87 < 2,51.

Поэтому по имеющимся данным на уров­не значимости α = 0,01 нельзя отклонить нулевую гипотезу о том, что генеральные средние равны, т.е. среднее время, затрачиваемое на ТО-1 по старой и новой методике, отличается незначимо, рас­хождения между ними случайны. Применение нового метода ТО-1 не позволяет снизить вре­мя обслуживания.

Ответ. На уровне значимости α = 0,01 нельзя утверждать о сокращении вре­мя обслуживания автомобилей по новой методике.

Задание 4.В рамках условия примера 2, определите, с точностью до минуты, насколько следует уменьшить время ТО-1, чтобы можно было бы отвергнуть нулевую гипотезу и принять конкурирующую гипотезу. Ответ. =46 мин.

Пример 3. Изменим условие предыдущего примера и положим, что те же статистические показатели были получены на выборках n _x =40 и n _y = 50.

Решение. Сформулируем нулевую и конкурирующую ги­потезы, исходя из условия задачи.

Н ₀: = — генеральные средние двух нормально распределенных совокупностей рав­ны, т.е. новая и старая методики по времени выполнения ТО-1 равнозначны.

Н ₁: > — генеральная средняя для X боль­ше, чем генеральная средняя для У, т.е. новая методики по времени выполнения ТО-1 дает выигрыш.

Так как конкурирующая гипотеза — правосторон­няя, то и критическая область — правосторонняя.

В качестве критерия для проверки этой гипоте­зы используется случайная величина u _нa6, вычисляемая по формуле

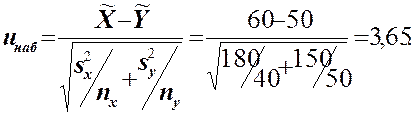
Заметим, что при правосторонней конкурирую­щей гипотезе Н ₁: и _кр следует находить по таблице функции Лапласа из ра­венства

Ф ₀(и _крпр) = (1 - 2 α)/2.

Отсюда

Ф₀(2,58) = 0,495.

Дата добавления: 2015-07-10