Формула Ейлера

Формула Ейлера має вигляд:

, (1.5)

де будь-яке дійсне число.

Зміст цієї рівності в тому, що вона визначає експоненту (за основою ) з чисто уявним показником, точніше, права частина в (1.5) просто позначена через , але це виправдано тим, що введений таким чином символ буде володіти властивостями експоненти в дійсній області.

За допомогою формул §§4.14,4.15,4.3 (приклад 3) безпосередньо перевіряються слідуючі властивості:

( ціле); .

Приклад. Обчислити .

Розв’язання.

4.20. Експонента e^z

Нехай 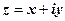. Покладемо . Ця рівність є означенням експоненти з будь-яким показником.

Основні властивості:

( ціле);

Для доведення використовуються властивості експоненти з дійсними і чисто уявними показниками (див.§1.17).

Приклад 1. Знайти .

Розв’язання. Якщо то

Відповідь:

Приклад 2. Обчислити .

Розв’язання.

Приклад 3. Показати, що якщо комплексне число, то

Розв’язання. Нехай Очевидно, що

Залишилось зауважити, що границя змінної величини дорівнює нулю тоді і тільки тоді, коли границя її модуля дорівнює нулю.

Дата добавления: 2015-07-12