Обчислення аргументу

Спочатку відмітимо властивість:

1) Аргумент дійсного і чисто уявного числа: якщо , то

2) Аргумент будь-якого числа можна знаходити за формулою:

(1.1)

Доведемо останню формулу у випадку, коли зображується точкою в другій чверті (рис.1.7). З . Оскільки , то

Рис 1.7

Інші випадки розміщення числа на площині розглядаються аналогічно.

Зауважимо, що вказаним способом для аргументу можна одержати формули, в яких використовуються арккотангенс, арккосинус чи арксинус.

Якщо не вимагається високої точності, то аргумент к.ч. можна знаходити графічно. З цією метою слід побудувати к.ч. на міліметровому папері і виміряти відповідний кут за допомогою транспортиру. Цей спосіб іноді використовують для грубої перевірки обчислень.

Приклад 1. Покажемо, як обчислюють аргументи чисел за допомогою формул цього пункту.

, (застосована формула (1.1), чверті);

, (формула (1.1), чверті);

, (формула (1.1), чверті);

, (формула (1.1), чверті);

Приклад 2. Достатньо встановити знаки дійсної і уявної частин к.ч., щоб перевірити рівності:

,

.

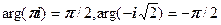Дата добавления: 2015-07-12