Tpигонометрична форма к.ч.

Нехай відомі модуль і аргумент к.ч. (див рис.1.5). Зауважимо, що 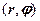- полярні координати точки 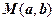, яка зображає число (якщо - полярна вісь).

У випадку розміщення осей і , вказаному на рис. 1.5, відомі формули переходу від полярних до прямокутних координат точки . Додамо ці рівності, помноживши другу на :

Остання форма запису комплексного числа називається тригонометричною. Як бачимо, щоб знайти тригонометричну форму, досить обчислити модуль і аргумент к.ч.

Приклади. Записати в тригонометричній формі слідуючі числа:

1) 2) 3)

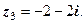
Розв’язання

1)

Відповідь:

2)

Відповідь:

3)

Відповідь: .

Розглянемо алгоритм переходу від алгебраїчної до тригонометричної форми к.ч.

Нехай дано к.ч. , на прикладі . Для переходу до тригонометричної форми необхідно:

1. Побудувати на площині ХОУ к.ч. і встановити, до якої чверті належить 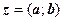. На даному прикладі: ІІІ четв. Див. рис.

2. Знаходимо модуль к.ч. за формулою (1)

(1)

На прикладі маємо:

3. За допомогою таблиць або мікрокалькулятора знаходимо , ураховуючи при цьому властивість

.

На прикладі: .

4. За формулою (1.1) § 1.14 знаходимо . Для даного прикладу: ІІІ чверті. Маємо:

5. Підставимо знайдені і у формулу

(2)

Для маємо:

Приклади для самостійного розв’язання

Представити у тригонометричній формі числа:

1. 2. 3. 4.

Відповіді. 1.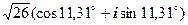

2.

3.

4.

4.16. Множення і ділення к.ч. в тригонометричній формі

Нехай числа записані в тригонометричній формі: .

Справедливі слідуючі формули:

Таким чином, при множенні (діленні) к.ч. їх модулі множаться (діляться), а аргументи додаються (віднімаються).

З’ясуємо геометричний зміст множення. Нехай (рис 1.8). Очевидно, що одержано поворотом на кут з подальшим розтягом (стиском) в разів.

Отже, множення к.ч. зводиться до повороту і розтягу (стиску) векторів.

Подібний зміст має і ділення к.ч.

Рис.1.8

Приклад. Використовуючи тригонометричну форму, обчислити добуток чисел 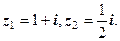З’ясувати геометричний зміст операції множення цих чисел.

Розв’язання.

З геометричної точки зору були виконані слідуючі перетворення (рис.1.9):

1) поворот вектора на кут результат повороту;

2) стиск (без зміни напряму) вектора в 2 рази 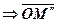- результат множення.

Рис.1.9

За допомогою рис.1.9 в даному випадку легко перевірити, що .

Приклади для самостійного розв’язання

1. Дані числа та . Необхідно:

1) перетворити їх у тригонометричну форму;

2) знайти їх добуток ;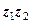

3) частку ;

4) зробити перевірку, виконавши ці дії над і в алгебраїчній формі.

2. Задовольнити умови прикладу 1, якщо , .

Відповіді.

1. 1) , ;

2) ;

3) .

2. 1) , ;

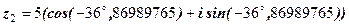2) ;

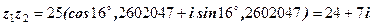3) .

4.17. Формула піднесення к.ч.до цілого степеня n

(Формула Муавра): якщо 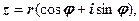то

(1.3)

Приклад. Нехай . Обчислити .

Розв’язання.

Подамо в тригонометричній формі: 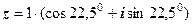застосовуємо формулу (1.3) при :

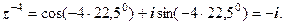
Приклади для самостійного розв’язання

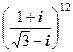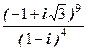Обчислити: 1. 2. 3.

Відповіді. 1. . 2. –1. 3. 104976.

4.18. Формула добування коренів

Формула добування коренів го степеня з числа

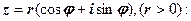
(1.4)

де символ означає корінь арифметичний з дійсного числа .

Таким чином, при має точно 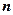значень.

Приклад. Знайти всі значення .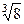

Розв’язання. Запишемо число 8 в тригонометричній формі:

Застосовуємо формулу (1.4) при 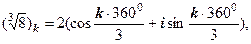де

Одержуємо три значення кореня:

Відповідь:

Приклади для самостійного розв’язання

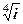Знайти всі значення коренів: 1. 2. 3. .

Відповіді. 1. , де k= 0, 1, 2. При k= 0: ;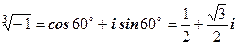

k= 1: ;

k= 2: .

2.

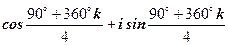= , де k= 0, 1, 2, 3.

При k= 0: ;

k= 1: ;

k= 2: ;

k= 3: .

3. ,

де k= 0, 1, 2, 3, 4, 5.

---

Дата добавления: 2015-07-12