Свойства основной моды. Для гауссова пучка можно записать выражение

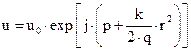
(6.29)

где r2=x2+y2. Параметр p - комплексный фазовый сдвиг при распространении света вдоль оси z, а q - комплексный параметр пучка, определяющий гауссово распределение поля по координате r, где r - расстояние от оси. Кроме того, q определяет кривизну волнового фронта, который вблизи оси является сферическим. Подставив выражение (6.29) в (6.28), получим

(6.30)

Штрих означает производную по z. Уравнение (6.30) эквивалентно двум уравнениям

	(6.31)
	(6.32)

Интегрируя (6.31), получаем

(6.33)

Это уравнение устанавливает весьма простое соотношение между параметром пучка в разных сечениях, отстоящих друг от друга на расстоянии z.

Когерентный световой пучок с гауссовым распределением поля имеет фундаментальное значение в теории волновых пучков. Этот пучок называют основной модой в отличие от других мод более высокого порядка, которые будут рассматриваться ниже. Вследствие особой важности рассмотрим свойства гауссова пучка с длиной волны l более подробно. Для этого выразим комплексный параметр q через два действительных параметра пучка R и w

(6.34)

Физический смысл этих параметров становится ясным при подстановке соотношения (6.34) в (6.29). Видно, что R есть радиус кривизны волнового фронта, а w характеризует изменение поля Е в поперечной плоскости. Распределение поля в этой плоскости, как видно из рис.1.6.в, подчиняется закону Гаусса и w равно расстоянию, на котором амплитуда поля убывает в е раз по сравнению с полем на оси.

Важно отметить, что гауссов характер распределение поля будет иметь в любой плоскости, будет меняться лишь ширина этого распределения. Параметр w принято называть радиусом пучка, а 2×w - диаметром пучка. В некоторой плоскости, называемой перетяжкой пучка, гауссов пучок стягивается к минимальному диаметру 2w₀. В этой плоскости, от которой целесообразно отсчитывать расстояние z, фазовый фронт является плоским и комплексный параметр пучка становится чисто мнимым

(6.35)

На расстоянии z от перетяжки

(6.36)

Из сопоставления соотношений (6.34) и (6.36) легко получить следующие важные в практическом отношении выражения:

	(6.37)
	(6.38)

Изменение радиуса, задаваемое выражением (6.37), графически иллюстрируется рис.6.10.

Рис.6.10. Продольная структура гауссова пучка: Ф - фазовый фронт, Г - перетяжка пучка.

Образующая пучка w(z) представляет собой гиперболу, асимптота которой наклонена к оси под углом

(6.39)

Этот угол равен углу дифракции основной моды в дальней зоне.

Для расчета комплексного фазового сдвига на расстоянии z от перетяжки пучка воспользуемся соотношениями (6.32) и (6.36); в результате получим

(6.40)

Интегрирование уравнения (6.40) дает

(6.41)

Действительная часть р представляет собой разность фаз Ф между гауссовым пучком и идеальной плоской волной, а мнимая - амплитудный фактор w₀/w, который характеризует уменьшение интенсивности на оси из-за расширения пучка. С учетом полученных соотношений выражение (6.26) принимает вид

(6.42)

где

(6.43)

Из формулы (6.43) видно, что Ф растет с увеличением z и уменьшением минимального радиуса пучка w0. Максимальное значение Ф равно p/2. Наличие в показателе экспоненты выражения (6.42) члена j×k×r2/2×R обусловлено отставанием по фазе световых колебаний на периферии гауссова пучка из-за кривизны волнового фронта.

Моды высших порядков. В предыдущем параграфе рассматривалось лишь одно решение уравнения (6.28), а именно гауссов пучок, являющийся основной модой свободного пространства. Существуют, однако, и другие решения уравнения (6.28), которым соответствуют пучки с сохраняющейся формой распределения амплитуды поля по поперечному сечению - высшие моды свободного пространства. Все решения (6.28) образуют полную ортогональную систему функций, поэтому любое произвольное распределение монохроматического поля может быть разложено по модам свободного пространства.

В прямоугольной системе координат x, y, z решение уравнения (6.28) может быть записано в виде

(6.44)

где g - функция x и z, а h - функция y и z. Для действительных g и h это решение описывает моды, поперечное распределение поля которых связано с радиусом гауссова пучка w(z). Подставляя (6.44) в (6.28), можно убедиться, что функция g и h удовлетворяют тому же самому дифференциальному уравнению, что и полиномы Эрмита Hn(t)

(6.45)

где n - целое число, а t=(2)^1/2×x/w для функции g и t=(2)^1/2×y/w для функции h. Таким образом

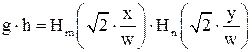
(6.46)

где m, как и n - целое число.

Физический смысл индексов m и n, называемых поперечными индексами моды, заключается в том, что они показывают, сколько раз поле меняет знак соответственно в направлении x и y. Важно отметить, что моды всех порядков характеризуются одним и тем же масштабным параметром w(z). Полиномы Эрмита низших порядков равны

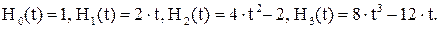
Для математического описания мод более высоких порядков можно использовать выражение (6.42), если в правую его часть вставить произведение g×h. Распределение поля в модах свободного пространства будет определяться, таким образом, произведением функций Эрмита и Гаусса

(6.47)

В частном случае m=0, n=0 мы имеем гауссов пучок - основную моду свободного пространства. Параметр R(z) в (6.47) для всех мод одинаков. Это означает, что кривизна волнового фронта одинакова для всех мод и закон его изменения один и тот же. Однако фазовый сдвиг Ф зависит от поперечного индекса. Можно найти, что

(6.48)

Из выражения (6.28) видно, что фазовая скорость с ростом индекса увеличивается.

Если решать уравнение (6.28) в цилиндрической системе координат r, j, z, подобное решение записывается в виде

(6.49)

После некоторых преобразований можно получить

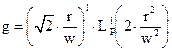
(6.50)

где L¹_p - обобщенный полином Лагерра, а р и l - соответственно угловой и радиальный индексы, показывающие, сколько раз поле меняет знак в радиальном и азимутальном направлениях.

Полиномы Лагерра низших порядков равны:

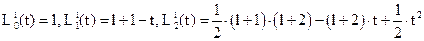
В цилиндрической системе координат, тем самым, моды будут описываться лагерро - гауссовыми функциями

(6.51)

Как и для случая прямоугольных координат, параметры w и R одинаковы для всех цилиндрических волн, а разность фаз, как и ранее, зависит от индексов моды и определяется уравнением

(6.52)

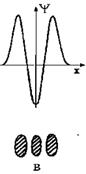
Графические распределения амплитуды поля для некоторых низших мод приведены на рис.6.11. Для наглядности под каждым графиком приведена картина, наблюдаемая на экране при падении на него светового пучка, соответствующего определенной моде.

Рис.6.11. Распределение амплитуды поля низших ТЕМmn –мод: а – ТЕМ00; б – ТЕМ10; в – ТЕМ20; г – ТЕМ30; д – ТЕМ40

Как эрмито-гауссовые, так и лагерро-гауссовые моды, реализуемые на практике, характеризуются, как правило, большим значением радиуса кривизны волнового фронта. Поэтому их с хорошей степенью приближения можно отнести к поперечным электромагнитным волновым пучкам вида ТЕМ. С учетом поперечных индексов эти пучки часто обозначаются как пучки ТЕМ_mn или ТЕМ_pl.

Следует, однако, помнить, что световые поля, записанные в виде (6.47) и (6.51), являются лишь приближенными решениями волнового уравнения. Степень приближения ухудшается с увеличением чисел (m+n) или (2p+l) и решение перестает быть верным, если величина, содержащая в качестве сомножителя сумму m+n+1 (либо 2p+l+1) становится сравнимой со значением k×z. Представление же произвольного поля в виде разложения по модам (6.47) и (6.51) является, следовательно, не строгим, а приближенным решением волнового уравнения. Если члены высокого порядка дают заметный вклад в разложение, то, чтобы ряд в целом был решением волнового уравнения, необходимо вводить дополнительные коэффициенты к членам ряда.

Дата добавления: 2015-07-11