
Читайте также:
|
Воспользуемся методами матричной оптики и элементами теории оптических резонаторов для оценки параметров лазерного излучения. Оценка выполняется в приближении, что внутри резонатора возбуждается основная мода ТЕМ00. На рис.6.25 показано схематически устройство типового оптического резонатора с активной средой.
Основные параметры оптического резонатора: длина резонатора – L; радиусы кривизны зеркал – r1 и r2. Активная среда имеет длину b и показатель преломления n.
Поскольку стрежень активной среды эквивалентен плоскопараллельной пластине, матрица перемещения луча между зеркалами резонатора, содержит приведенную длину

| (6.88) |
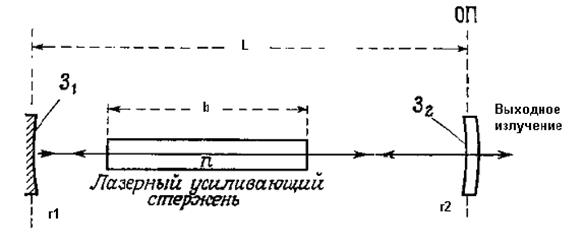
Рис.6.25
С учетом приведенной длины резонатора схема устройства приобретает вид, показанный на рис.6.26.
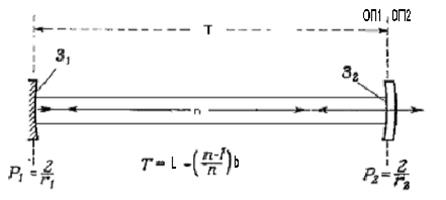
Рис.6.26
На рис.6.26 введены следующие обозначения: P1=2/r1 и P2=2/r2 – оптическая сила зеркал резонатора; Т - приведенная длина резонатора.
Нас интересует конфигурация световых волн излучаемых через выходное зеркало З2. Разместим опорную плоскость ОП1 на поверхности зеркала З2 и будем рассматривать исходный луч 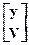 , который падает на ОП1 в положительном направлении оси z после выхода из активной среды. Часть энергии излучения после отражения от выходного зеркала З2 распространяется в обратном направлении. Излучение проходит через активную среду к зеркалу З1 системы, затем возвращается и вновь проходит через активную среду к выходному зеркалу.
, который падает на ОП1 в положительном направлении оси z после выхода из активной среды. Часть энергии излучения после отражения от выходного зеркала З2 распространяется в обратном направлении. Излучение проходит через активную среду к зеркалу З1 системы, затем возвращается и вновь проходит через активную среду к выходному зеркалу.
Если расположить вторую опорную плоскость ОП2 таким образом, что она совпадает с ОП1 то можно записать полную матрицу преобразования лучей М, связывающую опорные плоскости ОП1 и ОП2 и представляющую «полный проход» излучения через резонатор:

| (6.89) |
где A, B, C, D – постоянные оптических элементов модели резонатора (передаточные отношения оптических элементов).
Матрицу М, полученную в результате преобразований, следует проверить на равенство определителя единице, т.е. должно выполняться условие:

| (6.90) |
Если условие выполняется, тогда ее можно использовать в уравнении преобразования луча:

Мы фактически имеем достаточно информации для расчета одного прохода луча через данную систему.
Для того чтобы рассчитать изменение параметров луча вследствие N последовательных полных проходов через резонатор, нужно возвести полную матрицу преобразования лучей М в N–ю степень. С этой целью используем метод диагонализации матрицы:
 , ,  , , 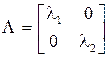
| (6.91) |
Собственные значения матрицы L, т.е. l1 и l2 можно определить, используя след матрицы М:

| (6.92) |
В зависимости от значения следа матрицы М резонатор относится к группе устойчивых или неустойчивых резонаторов.
Если выполняется условие

| (6.93) |
система относится к группе устойчивых резонаторов, в этом случае p>Q>0 и
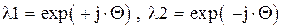
| (6.94) |
где величина Q определяется через тригонометрический косинус и след матрицы
 . .
| (6.95) |
Если система относится к группе неустойчивых резонаторов, выделяют два вида условий:
Ø  , тогда , тогда  ,
Ø ,
Ø  , тогда , тогда  , ,
| (6.96) |
где величина t определяется через гиперболический косинус и след матрицы
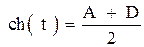 . .
| (6.97) |
Для конкретной геометрии системы, которую мы выбрали, можно определить число полных проходов (N) излучения через резонатор, для которого матрица преобразования лучей равна единичной матрице I, т.е.

| (6.98) |
В этом случае, какой бы параксиальный луч в резонаторе мы не выбрали, после N полных проходов через резонатор, его направление совпадает с первоначальным направлением.
Пусть М – унимодулярная матрица, с собственными значениями exp(±jQ), тогда можно записать:

| (6.99) |
Заменяя тригонометрические функции Q соответствующими гиперболическими функциями от t, этот же результат можно использовать для вычисления N-го прохода луча через неустойчивый резонатор:

| (6.100) |
Для неустойчивых резонаторов, конфигурация лазерного излучения подчиняется законам геометрической оптики. В этом случае отношения компонент собственных векторов равны  и
и  . В соответствии с приведенными выше рассуждениями эти отношения являются значениями
. В соответствии с приведенными выше рассуждениями эти отношения являются значениями 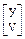 , или значениями радиуса кривизны (R) луча, распространяющегося через резонатор без изменения. Если внутри резонатора существует волновой фронт с такой кривизной, то он будет самовоспроизводиться.
, или значениями радиуса кривизны (R) луча, распространяющегося через резонатор без изменения. Если внутри резонатора существует волновой фронт с такой кривизной, то он будет самовоспроизводиться.
Рассмотрим теперь комплексное отношение компонент собственного вектора для устойчивого резонатора как значение q, которое определяет геометрию гауссова пучка, генерируемого в системе, если она работает в режиме возбуждения основной моды.
В соответствии с результатами, полученными выше, если матрица М описывает резонатор, и если ее два собственных значения равны exp (±jq), то значения q, сохраняющиеся при полном проходе резонатора, даются выражениями
 , ,
| (6.101) |
или, что эквивалентно
 , ,
| (6.102) |
причем p > Q > 0. Обращая уравнение (6.102) и учитывая (24), имеем
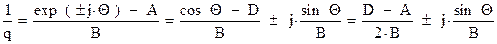
Из сравнения (6.102) и (6.34), получаем
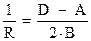 и и  . .
| (6.103) |
Можно показать, что отрицательная величина w2, отвечающая второму собственному значению, соответствует нереальному случаю, когда энергия пучка должна была бы сильно возрастать при удалении от оси. Отбрасывая это решение и оставляя только первое собственное значение  , находим характеристики основной моды гауссова пучка TEM00.
, находим характеристики основной моды гауссова пучка TEM00.
Радиус пучка во второй опорной плоскости задается выражением
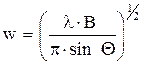 . .
| (6.104) |
Поверхности постоянной фазы этого пучка имеют кривизну
 . .
| (6.105) |
Радиус перетяжки пучка равен
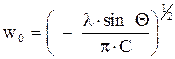 . .
| (6.106) |
Конфокальным параметром пучка определяется выражение
 . .
| (6.107) |
Положение перетяжки относительно второй опорной плоскости равно
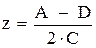 . .
| (6.108) |
Если z>0, тогда перетяжка смещена от опорной плоскости влево иначе, если z<0 – перетяжка смещена вправо от опорной плоскости.
Половина угла расходимости Q во второй опорной плоскости (в радианах) имеет вид
Дата добавления: 2015-07-11; просмотров: 98 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| МОДОВАЯ СТРУКТУРА ИЗЛУЧЕНИЯ ОПТИЧЕСКИХ РЕЗОНАТОРОВ | | | ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ ЛАЗЕРНЫХ РЕЗОНАТОРОВ |