
|
Читайте также: |
ОСНОВЫ ТЕОРИИ ОПТИЧЕСКИХ РЕЗОНАТОРОВ
ОБЩИЕ СВЕДЕНИЯ О РЕЗОНАТОРАХ
В §5. отмечалось, что генерация излучения в активной среде происходит, если инверсия среды обеспечивает превышение усиления над потерями. Так же отмечалось, что наибольшее распространение, для обеспечения этого условия, получило использование положительной обратной связи, т.е. резонаторов.
В широком смысле резонатором называют колебательную систему, в которой возможно накопление энергии акустических, механических и электромагнитных волн. Впервые резонаторы были использованы для возбуждения колебаний в радиотехнике. Резонаторы бывают активные и пассивные. Если внутри резонатора нет усиливающей активной среды, то такой резонатор называется пассивным, а при наличии усиления говорят об активных резонаторах. В приборах квантовой электроники обычно используются активные резонаторы. Среди активных резонаторов выделяют: закрытые, и открытые резонаторы. В закрытых резонаторах все три характерных размера соизмеримы с длиной волны излучения (l), что показано на рис.6.1.а. Такие резонаторы используются в устройствах СВЧ-диапазона. В квантовых приборах оптического диапазона используются открытые (оптические) (рис.6.1.б) резонаторы. Они, как правило, 1) не имеют боковой поверхности; 2) их размеры намного превышают длину волны излучения. В дальнейшем будем рассматривать только открытые (оптические) резонаторы, так как они имеют для нас наибольшее практическое значение.
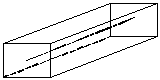 а.
а.
| 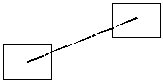 б.
б.
| 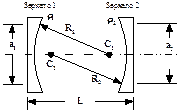
|
| Рис.6.1. Виды резонаторов: а - закрытый; б - открытый. | Рис.6.2. Структура оптического резонатора. |
Оптический резонатор представляет собой систему, состоящую из двух оптических зеркал (плоских или сферических) расположенных на некотором расстоянии друг от друга, что показано на рис.6.2. Все характеристики резонатора определяются следующими тремя комбинациями параметров: (g1×g2), (С1/g1), (С2/g2). Здесь g1 и g2 – обобщенные параметры резонатора, которые связаны с длиной резонатора L и радиусами кривизны зеркал следующим образом:
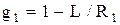 , , 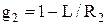
| (6.1) |
Величины C1 и C2 – циклические числа Френеля, определяемые по формуле:
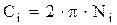 , ,
| (6.2) |
где Ni – число Френеля, равное
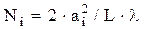 , ,
| (6.3) |
В выражении (6.3) 2×ai – апертурный размер резонатора, т.е. размер, ограничивающий поле резонатора. Таким образом, геометрия резонатора, определяющая его свойства, задается величинами: длиной резонатора L, радиусами кривизны зеркал R и апертурными размерами 2×ai.
Для качественной оценки резонатора удобно воспользоваться обобщенными параметрами резонатора g1 и g2 (g-фактором). На рис.6.3 приведена g - диаграмма оптических резонаторов. Каждой точке диаграммы соответствует резонатор определенной конструкции. Для области 0£g1g2£1 характерно наличие малых потерь (устойчивые резонаторы), а областям g1g2>1 и g1g2<0 - большие потери (неустойчивые резонаторы). Малые потери в резонаторе достигаются за счет того, что излучение, последовательно отражаясь от зеркал, остается все время в пределах ограниченной области внутри резонатора вблизи его оси. В резонаторах с большими потерями излучение после отражения от зеркал удаляется от его оси на неограниченное расстояние, что и приводит к большим потерям.
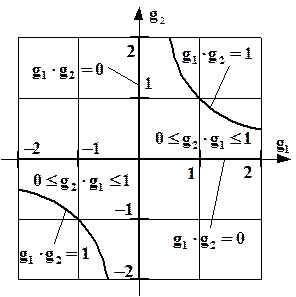
|
| Рис.6.3. G – диаграмма оптических резонаторов. |
Выделим наиболее распространенные виды оптических резонаторов.
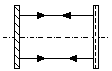
Плоскопараллельный резонатор (резонатор Фабри-Перо) (рис.6.4.а). Резонатор удовлетворяет следующим условиям: R2=R1=µ или g1=g2=1. Этот резонатор состоит из двух плоских зеркал, расположенных параллельно друг другу. В первом приближении стационарные волны такого резонатора можно представить как суперпозицию двух плоских электромагнитных волн, распространяющихся в противоположных направлениях вдоль оси резонатора.
Концентрический ( или сферический) резонатор (рис.6.4.б). Резонатор удовлетворяет кривым g1×g2=1, отделяющим области больших и малых потерь в резонаторе. Этот резонатор состоит из двух сферических зеркал, имеющих одинаковые радиусы кривизны R расположенные на расстоянии L друг от друга таким образом, что центры кривизны зеркал С1 и С2 совпадают (т.е. L=2×R или L=R1+R2). На рис.6.4.б показан также геометрический ход лучей в данном резонаторе. В этом случае волны представляют собой приближенно суперпозицию двух сферических волн, исходящих из точки С и распространяющихся в противоположных направлениях. Прямые g1=1 (R2=µ) и g2=1 (R1=µ) на рис.6.3 соответствуют полусферическим резонаторам. Если g1=-1, g2=-1 (L=2R1=2R2) – резонатор называют симметричный концентрический резонатор.
Конфокальный резонатор (рис.6.4.в). Он состоит из двух сферических зеркал с одинаковыми радиусами кривизны R, которые расположены на расстоянии L друг от друга таким образом, что фокусы зеркал F1 и F2 совпадают. Отсюда следует, что центр кривизны С одного зеркала лежит на поверхности второго зеркала (т.е. L=R). Положение конфокальных резонаторов описывается уравнением g2-0.5=0.25/(g1-0.5), являющимся уравнением гиперболы с центром в точке (0.5, 0.5). Если g1=0, g2=0 (R1=R2=L) – резонатор называют симметричный конфокальный резонатор.
| 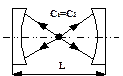
| 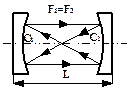
|
| а) | б) | в) |
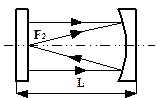
| 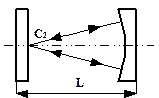
| 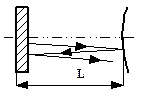
|
| г) | д) | е) |
| Рис.6.4. Виды оптических резонаторов. Здесь а - Плоский резонатор, б - Концентрический резонатор, в - Конфокальный резонатор, г - Полуконфокальный резонатор, д - Полусферический резонатор, е - Неустойчивый резонатор |
Резонаторы, состоящие из плоского и сферического зеркал. Примеры этих резонаторов показаны на рис.6.4.д (если g1=0.5, g2=1 или L=R2/2 либо g1=1, g2=0.5 или L=R1/2 - полуконфокальный) и рис.6.4.г (если g1=0, g2=1 (L=R1, r2=µ либо g1=1, g2=0 или L=R2, R1=µ - полуконцентрический). На этих же рисунках показаны и замкнутые траектории лучей в этих резонаторах.
Все рассмотренные выше оптические резонаторы являются примерами устойчивых оптических резонаторов, так как лучи в таких резонаторах остаются в пределах ограниченной области. Резонатор называется неустойчивым, когда произвольные лучи, последовательно отражаясь от каждого из зеркал, удаляются на неограниченно большое расстояние от оси резонатора. Пример неустойчивого оптического резонатора приведен на рис.6.4.е.
Оптические резонаторы обеспечивают необходимую для лазерной генерации положительную обратную связь и позволяют повысить плотность мощности светового поля до уровня, при котором происходит эффективный съем энергии с активной лазерной среды. Геометрия резонатора во многом определяет структуру лазерных пучков.
При рассмотрении свойств и особенностей резонаторов нас интересуют следующие вопросы: нормальные типы колебаний, которые существуют в резонаторе; распределение амплитуды и фазы этих колебаний на поверхности зеркал; величина дифракционных потерь и фазовые сдвиги, присущие каждому типу колебаний; частотный спектр и пространственное распределение выходящего из резонатора излучения.
Усиление и потери в оптическом резонаторе. Основным назначением оптического резонатора является создание условий, при которых возникающее внутри него индуцированное излучение многократно проходит через активную среду. Другими словами, задачей резонатора является осуществление положительной обратной связи за счет возвращения некоторой части распространяющегося между отражающими поверхностями излучения обратно в активную среду. Например, плоская электромагнитная волна, распространяющаяся в направлении перпендикулярном отражающим поверхностям, будет поочередно отражаться от них, усиливаясь при каждом последующем проходе. Учитывая это, одну из отражающих поверхностей делают частично отражающей для вывода излучения.
Мощность, генерируемая активными центрами среды в единице объема, определяется выражением
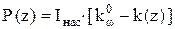 . .
| (6.4) |
Обозначим через Рген мощность, генерируемую во всем объеме активной среды, тогда
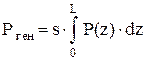 . .
| (6.5) |
Здесь s – площадь поперечного сечения активной среды, L – длина резонатора (для простоты, полагаем, что активная среда полностью занимает резонатор). Подставляя (6.4) в (6.5), находим
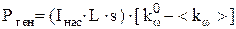 , ,
| (6.6) |
где <kw>=1/L×òLk0w(z)×dz – коэффициент усиления, усредненный по длине резонатора.
В случае стационарной генерации справедливо соотношение
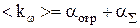 . .
| (6.7) |
Здесь aотр и aå - линейные коэффициенты ослабления мощности генерации, отвечающие соответственно потерям на отражение и суммарным потерям других видов. Учитывая (6.7), получаем из (6.5)
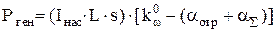 , ,
| (6.8) |
Этот результат позволяет сделать важное заключение: для обеспечения генерации необходимо, чтобы выполнялось неравенство
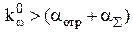 . .
| (6.9) |
Иными словами начальный коэффициент усиления должен превышать уровень потерь в резонаторе. Чем больше разность k0w-(aотр+aå), тем больше генерируемая мощность излучения. Порог генерации определяется равенством
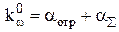 . .
| (6.10) |
Рассмотрим основные виды потерь резонатора. Потери на отражение обусловлены уходом части потока излучения из резонатора через зеркала («полезные потери»)
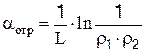 . .
| (6.11) |
Суммарные дополнительные потери («вредные потери») могут быть обусловлены поглощением излучения микрочастицами материальной среды, не являющимися активными центрами, рассеянием излучения через боковую поверхность активной среды, дифракционными эффектами, потери на торцах активной среды, потери из-за не параллельности зеркал резонатора и другими причинами.
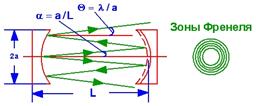
При прохождении фотонов через активную среду часть потока рассеивается на неоднородностях среды (рис.6.5), которые получили название - диссипативные потери.

| 
|
| Рис.6.5. Диссипативные потери в оптическом резонаторе. | Рис.6.6. Дифракционные потери резонатора. |
В этом случае ослабление потока фотонов за один проход можно оценить как
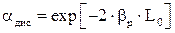
| (6.12) |
где bp - коэффициент рассеяния, L0 - длина активной среды.
Потери от разъюстировки зеркал резонатора связаные с наклоном зеркал резонатора на угол b относительно нормали к оси резонатора
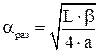
| (6.13) |
Особый интерес представляют дифракционные потери, которые могут выступать в одних случаях в роли дополнительных «вредных» потерь, а в других случаях – в роли «полезных» потерь. Они существенно зависят от величины апертуры.
Дифракционные потери резонатора обусловлены конечной величиной апертуры (диаметра) зеркал (рис.6.6). В результате дифракции происходит распространение волны в пределах некоторого малого угла q. Поэтому часть энергии на краю зеркала резонатора будет теряться при каждом отражении. Дифракционные потери весьма чувствительны к поперечной структуре поля излучения. Известно, что дифракционные потери aдиф зависят от числа Френеля Nф. Число Френеля Nф - число зон Френеля, которое видно на поверхности одного зеркала конечной апертуры из центра другого зеркала
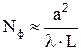
| (6.14) |
Чем больше зон Френеля перекрывает зеркало резонатора, тем меньше дифракционные потери. Для уменьшения дифракционных потерь необходимо выполнять условие N>>1. Коэффициент дифракционных потерь можно оценить по формуле
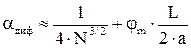 или или 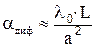
| (6.15) |
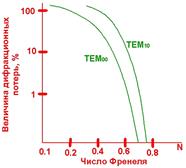
где jm»m×l/L – угол дифракции. Оценку дифракционных потерь выполняют часто графически, рис.6.7.
|
| Рис.6.7. Пример дифракционных потерь для различных мод резонатора. |
Для оценки резонатора с точки зрения вносимых им потерь используется понятие добротности резонатора
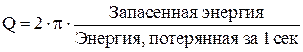 . .
| (6.16) |
При малых дифракционных потерях добротность резонатора выражается формулой
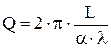 , ,
| (6.17) |
где a - коэффициент суммарных потерь за проход резонатора, l – длина резонатора.
Постоянная времени резонатора определяет переходной процесс в резонаторе, т.е. время, за которое плотность энергии в резонаторе уменьшается до уровня 1/e от исходного при отключении поля:
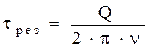
| (6.18) |
«Эффективное» число проходов излучения через резонатор, т.е. число проходов излучения, после которого устанавливаются колебания в резонаторе
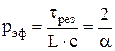
| (6.19) |
Формирование спектра излучения в оптическом резонаторе. Рассмотрим свойства оптического резонатора, предполагая наличие в нем плоских однородных волн конечного размера. Для устойчивого состояния таких волн в резонаторе необходимо, чтобы в нем образовались стоячие волны. Условие образования стоячих волн заключается в том, что расстояние между зеркалами должно быть равно целому числу полуволн, т.е.
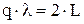 , ,
| (6.20) |
где q – целое число. Отметим, что условие резонанса выполняется и для волн, распространяющихся под определенными углами к оси резонатора:
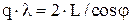 , ,
| (6.21) |
где j - угол между направлением распространения колебаний и осью резонатора. Таким образом, внутри резонатора образуется поле плоских волн, распространяющихся вдоль оси и под некоторыми дискретными углами к ней. Перепишем выражение (6.16) относительно частоты излучения
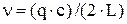 . .
| (6.22) |
Из (6.17) видно, что каждому значению q соответствует своя резонансная частота. Спектр резонансных частот эквидистантный и расстояние между частотами определяется выражением:
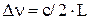 . .
| (6.23) |
Для того чтобы определить, сколько, резонансных частот будет одновременно существовать в резонаторе, необходимо знать ширину контура усиления рабочего (лазерного) перехода Dnконтур и величину суммарных внутренних потерь aS системы «активная среда + оптический резонатор». Возможны два случая:
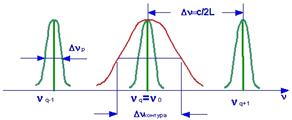
Ø ширина контура усиления меньше расстояния между двумя собственными частотами резонатора, т.е. Dnконтур£Dn (рис.6.8);
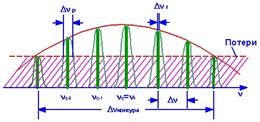
Ø в пределах контура усиления находится несколько собственных частот резонатора, Dnконтур>Dn (рис.6.9).
| 
|
| Рис.6.8. | Рис.6.9. |
В первом случае (одночастотная генерация), излучение будет квазимонохроматическим, т.е. первоначально за счет спонтанного излучения наблюдается генерация излучения во всем контуре спектральной линии. Однако резонатор вырезает узкую полосу частот Dnр, колебания в которой испытывают наибольшее усиление.
При увеличении длины резонатора возможна ситуация, когда пороговые условия самовозбуждения генерации могут быть выполнены для нескольких собственных частот резонатора. В этом случае спектр частот генератора определяется расположением частот относительно центра линии усиления и степенью взаимодействия колебаний связанных с этими частотами. Из рис.6.9 видно, что колебания, частота которых наиболее близка к центру линии излучения, имеют наибольшее усиление. При сильном взаимодействии (степень перекрытия собственных колебаний резонатора велика) насыщение усиления до уровня потерь приводит к последовательному затуханию всех колебаний, кроме одного, частота которого наиболее близка к центру линии усиления среды. При слабом взаимодействии колебаний (степень пространственного перекрытия колебаний мала) спектр излучения генератора является многочастотным. Таким образом, во - втором случае излучение становится более мощным, но менее монохроматичным.
Ширина резонансного пика Dnр – определяется добротностью резонатора Q:
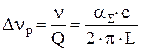 . .
| (6.24) |
В результате того, что наибольшее усиление получается в центре резонансного пика, спектральная линия излучения располагается в центре и имеет теоретическую ширину, которая определяется выражением:
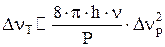 , ,
| (6.25) |
где Р – мощность излучения на данной линии.
Отметим еще раз факторы, определяющие частотные характеристики излучения квантовых приборов. Прежде всего, рабочий переход характеризуется естественной шириной контура Dnконтур. В реальных условиях за счет различных факторов контур уширяется. В пределах уширенной линии размещаются резонансные линии, число которых определяется шириной контура перехода и расстоянием между соседними пиками. В центре пиков располагаются узкие спектральные линии излучения, которые и определяют спектр выходного излучения прибора.
Дата добавления: 2015-07-11; просмотров: 457 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЗАПАСНЫЕ ЧАСТИ И ПРИНАДЛЕЖНОСТЬ | | | ФОРМИРОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛНОВЫХ ЛАЗЕРНЫХ ПУЧКОВ |