Систематизация факторов в АХД

Системный подход в АХД вызывает необходимость взаимосвя­занного изучения факторов с учетом их внутренних и внешних связей, взаимодействия и иерархии, что достигается с помощью их систематизации (структурирования). Структурирование — это раз­деление исследуемого показателя на множество составных элемен­тов (факторов) и выявление между ними взаимосвязи и соподчи-ненности.

Структурирование факторов в АХД осуществляется с помощью построения структурно-логической модели, которая дает возмож­ность установить наличие и направление связи не только между изучаемыми факторами и результативным показателем, но и меж­ду самими факторами. Структурно-логическая модель позволяет увидеть, что среди изучаемых факторов имеются такие, которые непосредственно влияют на результативный показатель, и такие, которые воздействуют не столько на результативный показатель, сколько друг на друга.

Различают детерминированные и стохастические структурно-логические факторные модели.

Создать детерминированную факторную систему — значит пред­ставить изучаемое явление в виде алгебраической суммы, частного или произведения нескольких факторов, определяющих его величину и находящихся с ним в функциональной зависимости.

Например, объем выпуска продукции промышленного предпри­ятия можно представить в виде произведения двух факторов перво­го порядка: среднегодового количества рабочих и среднегодовой выработки продукции одним рабочим, которая, в свою очередь, за­висит непосредственно от количества отработанных дней одним рабочим в среднем за год и среднедневной выработки продукции рабочим. Последняя также может быть разложена на продолжитель­ность рабочего дня и среднечасовую выработку (рис. 3.5).

Развитие детерминированной факторной системы достигается, как правило, за счет детализации комплексных факторов. Элемент-

				Валовой	выпуск
		продукции (ВП)
Среднесписочная численность рабочих {ЧР)
		Среднегодовая выработка одного среднесписочного рабочего (ГВ)

Среднедневная выработка одного рабочего (ДВ)

Количество отработанных дней одним рабочим за год (Д)

Среднечасовая выработка одного рабочего (ЧВ)

Средняя продолжительность рабочего дня, ч (П)

Рис. 3.5. Детерминированная структурно-логическая факторная модель валового выпуска продукции

ные факторы (в нашем примере — количество рабочих, количество отработанных дней, продолжительность рабочего дня) не расклады­ваются на сомножители. С развитием системы комплексные факторы постепенно детализируются на менее общие, те, в свою очередь, — еше на менее общие, постепенно приближаясь по своему аналитиче­скому содержанию к элементным (простым).

Однако развитие факторных систем до необходимой глубины связано с некоторыми методологическими трудностями, и прежде всего с трудностью нахождения факторов общего характера, кото­рые можно было бы представить в виде алгебраической суммы, частного или произведения нескольких факторов. Поэтому обыч­но детерминированные системы охватывают наиболее общие фак­торы. Между тем исследование более конкретных факторов в АХД имеет существенно большее значение, чем исследование общих факторов.

Отсюда следует, что совершенствование методики факторного анализа должно быть направлено на взаимосвязанное изучение конкретных факторов, которые находятся, как правило, в стоха­стической связи с результативными показателями.

Структурирование факторов играет большую роль не только в детерминированном, но и в стохастическом анализе. Оно позво­ляет установить наличие или отсутствие причинно-следственных связей между исследуемыми показателями, изучить направление связи, форму зависимости ит.д., что очень важно при определении степени их влияния на изучаемое явление и при обобщении ре­зультатов анализа.

На рис. 3.6 вкачестве примера показана связь между себесто­имостью единицы продукции растениеводства и такими фактора-

54

55

		• L		•.	1
	Количество внесенных удобрений	>	Урожайность культур	... > Производительность 4— труда
				,	L	.	Т
Качество			Уровень механизации производства
посевного материала

Рис. 3.6. Структурно-логическая модель стохастической факторной системы себестоимости продукции земледелия

ми, как урожайность культур, производительность труда, количе­ство внесенного удобрения, качество семян, степень механизации производства.

Прежде всего необходимо установить наличие и направление свя­зи между себестоимостью продукции и каждым фактором. Без­условно, между ними существует тесная связь. Непосредственное влияние на себестоимость продукции оказывает в данном примере только урожайность культур. Все остальные факторы влияют на се­бестоимость продукции не только прямо, но и косвенно — через уро­жайность культур и производительность труда. Например, количество внесенных удобрений в почву содействует повышению урожайности культур, что при прочих одинаковых условиях обусловливает сниже­ние себестоимости единицы продукции. Однако необходимо учиты­вать и то, что увеличение количества внесенных удобрений приводит к росту суммы затрат на гектар посева. И если сумма затрат возраста­ет более высокими темпами, чем урожайность, то себестоимость про­дукции будет не снижаться, а повышаться. Значит, связь между этими двумя показателями может быть и прямой и обратной. Аналогично влияет на себестоимость продукции и качество семян. Приобретение элитных, высококачественных семян вызывает рост суммы затрат. Если затраты возрастают в большей степени, чем урожайность от применения более высококачественных семян, то себестоимость продукции будет повышаться, и наоборот.

Степень механизации производства влияет на себестоимость продукции и прямо и косвенно. Повышение уровня механизации вызывает рост затрат на содержание основных средств производ­ства. Однако при этом увеличивается производительность труда, растет урожайность, что содействует снижению себестоимости продукции.

Исследование взаимосвязей между факторами показывает, что все факторы прямо или косвенно влияют друг на друга. Из всех изучаемых факторов отсутствует причинно-следственная связь только между качеством семян, количеством удобрений и механи­зацией производства. Именно эти факторы следует отобрать для корреляционного анализа себестоимости продукции, поскольку в многофакторную корреляционную модель рекомендуется вклю­чать невзаимосвязанные факторы.

Таким образом, систематизация факторов позволяет более глу­боко изучить взаимосвязь факторов при формировании величины изучаемого показателя, что имеет немаловажное значение на сле­дующих этапах анализа, особенно на этапе моделирования иссле­дуемых показателей.

3.7. Детерминированное моделирование

и способы преобразования факторных систем

Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, определяющими их величину.

Моделирование — это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаи­мосвязь исследуемого показателя с факторными передается в форме конкретного математического выражения.

Моделирование экономических процессов играет исключитель­но важную роль в АХД. С его помощью достигается предельно точ­ная формулировка методики анализа, приводятся в систему мысли и суждения.

В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помо­щью детерминированных факторных моделей исследуется функ­циональная связь между результативным показателем (функцией) и факторами (аргументами).

При создании детерминированных факторных моделей необ­ходимо выполнять ряд требований:

1) факторы, включаемые в модель, должны реально существо­вать, а не быть надуманными абстрактными величинами или яв­лениями;

2) факторы, входящие в модель, должны находиться в причин­но-следственной связи с изучаемым показателем. Факторные мо-

56

57

дели, которые отражают причинно-следственные отношения меж­ду показателями, имеют значительно большее познавательное значение, чем модели, созданные при помощи приемов математи­ческой абстракции. Последнее можно проиллюстрировать следу­ющим образом. Возьмем две модели:

ВП = ЧР * ГВ;

Г В = ВП: ЧР,

где ВП — валовой выпуск продукции предприятия; ЧР— численность работников на предприятии; Г В — среднегодовая выработка продукции одним работни­ком. В первой модели факторы находятся в причинной связи с ре­зультативным показателем, а во второй — в математическом соот­ношении. Значит, вторая модель, построенная на чисто математи­ческих зависимостях, имеет меньшую познавательную и практи­ческую ценность, чем первая;

3) все показатели факторной модели должны быть количе­ственно измеримыми, т.е. иметь единицу измерения и необходи­мую информационную базу;

4) факторная модель должна обеспечивать возможность изме­рения влияния отдельных факторов, т.е. в ней должна учитываться соразмерность изменений результативного и факторных показате­лей, а сумма влияния отдельных факторов должна равняться об­щему приросту результативного показателя.

В детерминированном анализе выделяют следующие типы наи­более часто встречающихся факторных моделей.

1. Аддитивные модели:

Y = =х_]+х₂ +... + х_n

Они используются в тех случаях, когда результативный показа­тель представляет собой алгебраическую сумму нескольких фак­торных показателей.

2. Мультипликативные модели:

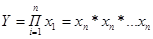
Этот тип моделей применяется в том случае, когда результатив­ный показатель представляет собой произведение нескольких фак­торных показателей.

3. Кратные модели:

Они применяются в том случае, когда результативный показа­тель получают делением одного факторного показателя на величи­ну другого.

4. Смешанные (комбинированные) модели — сочетание в различ­ных комбинациях предыдущих моделей:

Y=(a+b)c и т.д.

Дата добавления: 2015-10-21