Задача 11.

1. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода 1 час, а второго 2 часа.

2. Дано уравнение ax=b. Если числа a и b выбираются в промежутках 0<a<8, 0<b<10, то какова вероятность того, что корень уравнения будет больше 1?

3. На отрезок АВ длиной 10 см бросают наугад точку М. Какова вероятность того, что площадь квадрата со стороной АМ будет больше 25см и меньше 64см.

4. Числа a и b выбирают случайно в промежутке [-1,1]. Найти вероятность того, что корни уравнения действительны.

5. В условиях варианта 7 найти вероятность того, что корни уравнения положительные.

6. В условиях варианта 7 найти вероятность того, что корни уравнения отрицательные.

7. В условиях варианта 7 найти вероятность того, что корни уравнения комплексные.

8. Две одинаковые монеты радиуса 2 расположены внутри круга радиуса R, в который наугад бросают точку. Какова вероятность того, что точка попадет на одну из монет, если монеты не перекрываются.

9. Шар радиуса R брошен в квадратную проволочную сетку, сторона которой 6R. Какова вероятность того, что шар не заденет сетки.

10. На отрезке АВ наугад поставлены 2 точки L и M. Какова вероятность того, что точка L будет ближе к точке M, чем к точке А.

11. На отрезке длиной L наугад выбраны 2 точки. Какова вероятность того, что расстояние между ними меньше k*L, где . Вычислить при k=1/2.

12. Точка брошена наудачу внутрь круга радиуса R. Найти вероятность того, что точка находится от центра этого круга на расстоянии меньше r (r<R). Вычислить при R=2r.

13. Найти вероятность того, что сумма двух наугад выбранных положительных правильных дробей не больше 1, а произведение не больше 0,3.

14. Наугад взяты два положительных числа, каждое из которых не превышает двух. Найти вероятность того, что их произведение не больше 1, а частное не больше двух.

15. Какова вероятность того, что сумма двух положительных правильных дробей не превышает 1, а произведение не больше 2/3.

16. Сумма квадратов двух неотрицательных действительных чисел не больше 6. Какова вероятность того, что сумма этих чисел не больше 8?

17. Стержень длиной 200 мм наудачу ломается на части. Определить вероятность того, что хотя бы одна часть стержня между точками излома будет не более 10 мм, если точек излома две (излом равновозможен в любом месте).

18. Задача 21 при условии, что точек излома три

19. Определить вероятность того, что корни квадратного уравнения 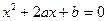вещественны, если значения коэффициентов равновозможны в прямоугольнике ½a½£ n ½ b ½£ m

20. На окружности радиуса R наудачу поставлены три точки А, В, С. Какова вероятность того, что треугольник АВС остроугольный.Н

21. На отрезке АВ длиной L поставлены две точки M и N. Определить вероятность того, что длины каждого из трех получившихся отрезков не превосходят заданной величины a (L³ a ³L/3)

22. Какова вероятность того, что из трех взятых наугад отрезков длиной не более L можно построить треугольник.

23. К автобусной остановке через каждые четыре минуты подходит автобус линии А и через каждые 6 минут автобус линии В. Интервал времени между моментами прихода автобуса линии А и ближайшего следующего прихода автобуса линии В равновозможен в пределах от 0 до 4 минут. Определить вероятность того, что первый подошедший автобус окажется автобусом линии А.

24. В условиях задачи 2 определить вероятность того, что автобус какой либо линии подойдет в течение двух минут.

25. Противотанковые мины поставлены по прямой линии через 15м. Танк шириной 3 м движется перпендикулярно прямой. Какова вероятность того, что он подорвется.

Дата добавления: 2015-10-21