Читайте также:
|
Типовой расчет по теории вероятностей N1
(Ответы сопровождать объяснениями.)
Задача 1
1. Сколько существует трехзначных чисел, которые записываются с помощью цифр 0,1,2,3,4,5 и делятся на 3?
2. В клубе велосипедистов при выступлении каждому члену выдается 3-значный номер. Из-за суеверия в номерах не используется цифра 8. Сколько членов было в клубе, если использованы все трехзначные номера.
3. В восьмеричной системе счисления восемь цифр (0,1,...,7). Сколько в восьмеричной системе чисел, записываемых тремя знаками.
4. При проведении первенства по футболу в высшей лиге, состоящей из 17 команд ее должны покинуть четыре команды, занявшие последние места (14-17). Сколькими способами это может быть сделано.
5. Сколькими способами можно выбрать 12 человек из 17, если данные два человека не могут быть выбраны вместе.
6. В лифт (m+1) этажного дома вошли n человек. Каждый может выйти на любом из этажей, начиная со второго. Сколько существует различных способов выхода?
7. Сколькими способами две пары близнецов можно рассадить на четырех местах?
8. Сколькими способами можно разделить колоду из 36 карт пополам, так, чтобы в каждой части было по 2 туза?
9. Сколькими способами 7 студентов можно поселить в одноместную 2-местную и 4-местную комнаты в общежитии?
10. Сколькими способами можно поставить белую и черную ладью, так чтобы они не били друг друга.
11. Сколькими способами можно поставить белого и черного слона, так чтобы они не били друг друга?.
12. Сколькими способами можно поставить белого и черного ферзя, так чтобы они не били друг друга?
13. Сколькими способами можно поставить белого и черного короля, так чтобы они не били друг друга?
14. Сколько слов длины n можно образовать, используя алфавит из m букв?
15. Сколько имеется четырехзначных чисел у которых каждая следующая цифра больше предыдущей;
16. Сколько имеется четырехзначных чисел у которых каждая следующая цифра меньше предыдущей
17. Сколькими способами можно составить ожерелье из 5 бусин синего цвета, 6 бусин красного цвета и 7 бусин зеленого цвета?
18. Сколькими способами можно рассадить гостей за круглым столом? Предполагается, что стол может вращаться, и способы переходящие друг в друга при вращении стола считаются совпадающими.
19. Сколько существует различных матриц размера 
с элементами 
?
20. Пусть множество A содержит n элементов, множество B− m элементов. Сколько существует бинарных отношений на множествах A, В? (Бинарным отношением называется произвольное подмножество декартова произведения 
).
Задача 2(*)
1. Сколько существует различных матриц размера с элементами с попарно различными строками?
2. Пусть множество A содержит n элементов, множество B m элементов. Сколько существует функций из A в B?
3. Сколько существует булевых функций от n переменных?
4. Сколько существует булевых функций от n переменных, сохраняющих 0, то есть удовлетворяющих условию 
?
5. Сколько существует булевых функций n переменных, сохраняющих единицу, то есть удовлетворяющих условию 
?
6. Сколько существует самодвойственных булевых функций от n переменных. Функция называется самодвойственной, если она удовлетворяет условию 
.
7. Сколько существует линейных булевых функций от n переменных. Функция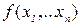 
называется линейной, если она представима в виде 
, где 
означает сложение по модулю 2, 
8. Пусть множество A содержит n элементов. Сколько существует рефлексивных бинарных отношений на множестве A? (Отношение 
называется рефлексивным, если 
для всех 
).
9. Пусть множество A содержит n элементов. Сколько существует симметричных бинарных отношений на множестве A? (Отношение 
называется симметричным, если 
для всех 
).
10. Пусть множество A содержит n элементов. Сколько существует антирефлексивных бинарных отношений. (Отношение называется рефлексивным, если 
для всех ).
11. Сколько существует антисимметричных бинарных отношений на множестве А. (Отношение называется антисимметричным, если 
для всех ).
12. Пусть множество A содержит n элементов. Сколько существует рефлексивных и симметричных одновременно бинарных отношений?
13. Пусть множество A содержит n элементов. Сколько существует бинарных отношений на множестве A, не являющихся симметричными?
14. Пусть множество A содержит n элементов. Сколько существует бинарных отношений на множестве A, не являющихся рефлексивными?
15. Сколькими способами 3n предметов можно разложить поровну по n урнам, если а) урны различны; б) урны одинаковы?
16. Имеется n различных предметов и n одинаковых предметов. Сколькими способами можно разложить в ряд 2n предметов.
17. Имеется n различных предметов и n одинаковых предметов. Сколькими способами можно выбрать из них n предметов.
18. Сколькими способами можно представить число n в виде суммы трех натуральных слагаемых.
19. Сколько положительных целочисленных решений имеет система 
Дата добавления: 2015-10-21; просмотров: 241 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Характеристики различных типов производства | | | Задача 3 |