
Читайте также:
|
Задачей эксперимента является нахождение истинного значения x 0 физической величины, которое может быть найдено, если имеется генеральная совокупность всех значений искомой величины Х. Однако, в связи с тем, что количество наблюдений в выборке конечно, в опыте находят некоторое приближенное к x 0 значение 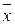 , называемое оценкой истинного значения, и указывают интервал, в который истинное значение x 0 попадает с заданной вероятностью P. Этот интервал называют доверительным интервалом, а вероятность Р – доверительной вероятностью.
, называемое оценкой истинного значения, и указывают интервал, в который истинное значение x 0 попадает с заданной вероятностью P. Этот интервал называют доверительным интервалом, а вероятность Р – доверительной вероятностью.
 В качестве оценки истинного значения согласно (2.2) выбирают среднее арифметическое результатов наблюдений в выборке
В качестве оценки истинного значения согласно (2.2) выбирают среднее арифметическое результатов наблюдений в выборке
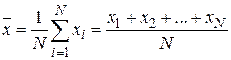 , (2.7)
, (2.7)
которое называют выборочным средним. Среднее 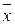 также является случайной величиной, и если повторить опыт по его нахождению несколько раз, то получим выборку средних X:
также является случайной величиной, и если повторить опыт по его нахождению несколько раз, то получим выборку средних X: 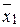 ,
, 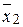 ,...,
,..., 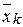 , которые также будут отличаться друг от друга случайным образом, однако разброс средних значений будет заметно меньше разброса результатов отдельных наблюдений в каждой выборке.
, которые также будут отличаться друг от друга случайным образом, однако разброс средних значений будет заметно меньше разброса результатов отдельных наблюдений в каждой выборке.
Для нахождения доверительного интервала необходимо знать распределение средних значений 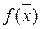 около x 0. Зная вид
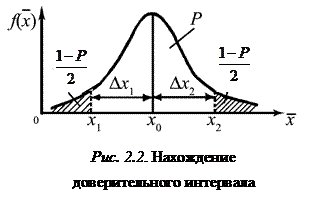
около x 0. Зная вид 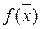 , можно построить интервал, в который истинное значение x 0 попадает с вероятностью Р. Для этого на оси абсцисс (рис. 2.2) находят точки x 1 и x 2 такие, чтобы площади под графиком
, можно построить интервал, в который истинное значение x 0 попадает с вероятностью Р. Для этого на оси абсцисс (рис. 2.2) находят точки x 1 и x 2 такие, чтобы площади под графиком 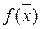 слева от x 1 и справа от x 2 равнялись бы одной и той же величине
слева от x 1 и справа от x 2 равнялись бы одной и той же величине  . Тогда площадь под графиком
. Тогда площадь под графиком 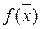 в интервале (x 1, x 2) будет равна значению вероятности P, и для произвольного полученного в опыте среднего значения можно написать: x 1 <
в интервале (x 1, x 2) будет равна значению вероятности P, и для произвольного полученного в опыте среднего значения можно написать: x 1 < 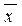 < x 2 c вероятностью Р:
< x 2 c вероятностью Р:
 . (2.8)
. (2.8)
Границы интервала можно также записать в виде  ,
, 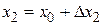 . Если распределение
. Если распределение 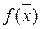 симметрично, то
симметрично, то 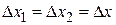 . Величину
. Величину  в этом случае называют случайной доверительной погрешностью результата измерения.
в этом случае называют случайной доверительной погрешностью результата измерения.
Дата добавления: 2015-10-21; просмотров: 103 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Случайная величина. Генеральная совокупность и выборка | | | Нормальное или гауссовское распределение |