
Өлшеу қателіктері әдетте түрлі факторлардың әсерінен орын алады да, негізінен екі топқа бөлінеді: кездейсоқ және систематикалық.
Егер де бір шаманы бірнеше қайталап өлшеу барысында орын алған қателіктер тұрақты мән алса, немесе белгілі бір заңдылықпен өзгерсе, онда ондай қателікті систематикалық қателік деп атайды. Систематикалық қателік өлшемінің номиналдық мәнінің өзгеріске ұшырап кету салдарынан туындайды. Систематикалық қателік сонымен қатар өлшеу тәсілдерінен кететін қателік, (тәсілдік қателік) өлшеу құралдарының конструктивтік кемшіліктерінен, олардың сипаттамларының өзгеріске ұшырауынан, оператордың өлшеуді дұрыс жүргізбеу салдарынан да туындайды.
Систематикалық қателіктер өз кеегінде тұрақты және айнымалы болып бөлінеді. Тұрақты қателіктер аспап стрелкаларының қисаю салдарынан, аспаптарды дұрыс емес градуиовкалау т.с.с. салдардан туындайды.
Айнымалы қателіктердің ішінен прогрессті түрде өзгермелі, монотонды өспелі немесе кемімелі, периодты түрде өзгермелі қателіктерді атап өтуге болады. Систематикалық қателіктерді аспаптарға сәйкескенше түзетулер енгізу, компенсациялау т.с.с. тәсілдерді қолдану арқылы жоюға болады.
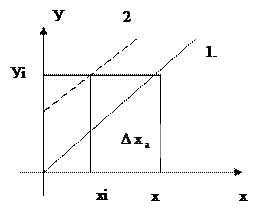 Өлшеу құралдарына түрлі факторлар әсер ету салдарынан, оның сипаттамасы өзгеріске ұшырауы мүмкін. Бұл жағдайда аддитивті (2.1- сурет), мультипликативті (2.2- сурет) және бейсызықты қателіктер (2.3- сурет) орын алуы мүмкін.
Өлшеу құралдарына түрлі факторлар әсер ету салдарынан, оның сипаттамасы өзгеріске ұшырауы мүмкін. Бұл жағдайда аддитивті (2.1- сурет), мультипликативті (2.2- сурет) және бейсызықты қателіктер (2.3- сурет) орын алуы мүмкін.

2.1-сурет. Аддитивті қателік ∆ ха 1 – идеал сипаттама, 2 – аддитивті қателігі бар сипаттама
Кездейсоқ қателіктерді сипаттау.
Кездейсоқ қателіктерді сипаттау үшін «таралымның дифференциялдық функциясы» деген ұғым енгізілді.
Қалыпты заңдылық (Гаусс заңдылығы) үшін бұл функция былайша жазылады.
–(х-m)2/2δ2х
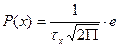
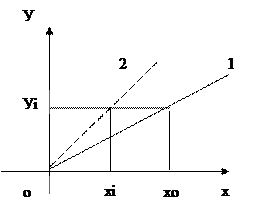
Мұндағы m – өлшенетін кездейсоқ шаманың X – математикалық күтімі, T 
 - кездейсоқ шаманың Х орта квадраттық ауытқуы.
- кездейсоқ шаманың Х орта квадраттық ауытқуы.
 |
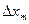
 2.2- сурет. Мультипликативті қателік ∆ хм. 1 – идеал сипаттама, 2 – мультипликативті қателігі бар сипаттама.
2.2- сурет. Мультипликативті қателік ∆ хм. 1 – идеал сипаттама, 2 – мультипликативті қателігі бар сипаттама.
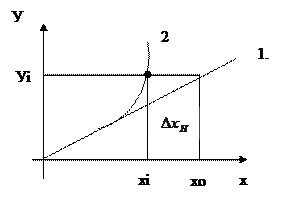
2.3- сурет. Бейсызықтық қателік ∆ хн.. 1 – идеал сипаттама, 2 – бейсызықтықтан болатын қателік.
Қалыпты заңның дифференциялдық функциясы 2.4- суретте келтірілген, әдетте сурет ауданы


2.4- сурет. Кездейсоқ қателіктердің қалыпты таралымы.
Сол сияқты, кездейсоқ қателіктердің [х1, х2] кескіндісіне түсу ықтималдығы, суреттегі штрихтелген фигураның ауданымен анықталады, яғни

Систематикалық және кездейсоқ қателіктерді бағалау кезінде өлшеу нәтижелерінің математикалық күтімі деген ұғым қолданылады.
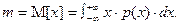
Систематикалық қателікті өлшенетін шаманың нақты мәні мен өлшеу нәтижелерінің математикалық күтімінің арасындағы ауытқу арқылы анықтауға болады.
Ө= М[Х]]- Хд
Ал кездейсоқ қателік - өлшеу нәтижесінің дара мәндері мен математикалық күтімінің арасындағы ауытқу арқылы сипатталады
δ = Х - М[Х]
Өлшеу нәтижелерінің математикалық күтім төңірегінде қаншалықты шашырап орындалуын сипаттайтын шама дисперсия.

Және орта квадраттық ауытқу
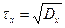
Егерде өлшеу нәтижелеріне систематикалық қателіктер енбеген жағдайда, кездейсоқшаманың математикалық күтімі өлшенетін шаманың нақты мәні болып табылады.
Өлшеу нәтижелерін бағалау нүктелік немесе интервалдық тәсілдермен іске асады. Мысалы, өлшеу нәтижелерінің сандары N – ге тең болсын, Х: х1, х2 ……..хN . Бағаланатын параметрлерге математикалық күтім мен орта квадраттық ауытқу жатады. Оценка а – параметрінің бағалануы а0 нүктелік болып табылады, егерде ол тек қана бір цифрмен айқындалса. Математикалық күтімнің m және дисперсияның Дх нүктелік бағалануы келесі формулалармен анықталады.
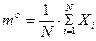
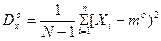
Интервалдық бағалау кезінде, өлшенетін шаманың нақты мәнін қамтитындай интервал табылады. Бұл интервалды сенімділік интервалы (доверительный интервал) дейміз.
Өлшенетін шаманың сенімділік интервалында жату ықтималдығын, сенімділік ықтималдылығы (доверительная вероятность) деп атайды. Мысалға, кездейсоқ шаманың таралымы қалыпты заңға бағынсын, дисперсияға Дх=δХ2. Бұл жағдайда математикалық күтімнің m (m-δх0;m+δх0) интервалына түсу ықтималдығы келесі өрнектен анықталады
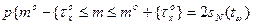
Мұндағы 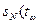 )– Стьюдент таралымы, δх0 – таңдамалы таралымының орта квадраттық ауытқуы, m0 – таңдамалы таралымының математикалық күтімі,;
)– Стьюдент таралымы, δх0 – таңдамалы таралымының орта квадраттық ауытқуы, m0 – таңдамалы таралымының математикалық күтімі,;

Егер сенімділік ықтималдылығы р және n=N-1 мәні белгілі болса, онда Стьюдент таралымының кестесінен tа - шамасын табамыз. Бұл жерде

Таңдамалы таралымның дисперсия үшін (орта квадраттық ауытқу δх) сенімділік интервалы келесі қатынастан анықталады.
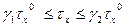
Мұндағы  және
және 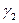 Пирсон таралымынан (Х2 - таралымы) табылатын шамалар (әдейіленген кесте көмегімен).
Пирсон таралымынан (Х2 - таралымы) табылатын шамалар (әдейіленген кесте көмегімен).
Интервалдық бағалау қайталап өлшеу сандары шектелген жағдайда (N<30) қолданылады. Егерде тәжірибе саны жеткілікті болған жағдайда(N>30) Стьюдент таралымы қалыпты таралымға айналады, бұл жағдайда 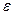 және
және  ,
, 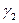 шамаларын анықтаудың қажеті болмай қалады.
шамаларын анықтаудың қажеті болмай қалады.
Өлшеу құралдарының қателіктерін қосу.
Өлшеу құралдарының қорытқы қателігі, құрал құрамына кіретін элементтер қателіктерінің қосындысымен айқындалады, сол себептен қателіктерді қосу белгілі бір ереже бойынша орындалуы қажет. Қосу барысында систематикалық және кездейсоқ қателіктер өз алдына, мультипликативтік және аддитивтік қателіктер өз алдына қосылады.
Систематикалық қателіктер келесі формула арқылы қосылады.
 =
= 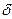 1
1 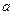 1 +
1 + 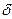 2
2 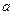 2 + …
2 + … 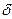 .n
.n 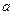 n
n
Мұндағы  - салыстырмалық қателіктерді қосу үшін, олардың таралым заңдылықтарының қосындысын айқындау қажет. Бұл мәселе кездейсоқ қателіктер саны 3-4 тен асып кетсе өте қиын шешіледі. Сондықтан, есептеуді жеңілдету үшін кездейсоқ қателіктердің өзара байланыс дәрежелерін анықтайды және де кездейсоқ қателіктерді аддитивті және мультипликативті құрамдарға бөлу қажет. Аддитивті және мультипликативті қателіктер жеке- жеке қосылады. Кездейсоқ қателіктің қорытқы мәні (қосындысы) келесі формуламен анықталады.
- салыстырмалық қателіктерді қосу үшін, олардың таралым заңдылықтарының қосындысын айқындау қажет. Бұл мәселе кездейсоқ қателіктер саны 3-4 тен асып кетсе өте қиын шешіледі. Сондықтан, есептеуді жеңілдету үшін кездейсоқ қателіктердің өзара байланыс дәрежелерін анықтайды және де кездейсоқ қателіктерді аддитивті және мультипликативті құрамдарға бөлу қажет. Аддитивті және мультипликативті қателіктер жеке- жеке қосылады. Кездейсоқ қателіктің қорытқы мәні (қосындысы) келесі формуламен анықталады.
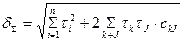
мұндағы  - кездейсоқ шамалардың арасындағы өзара байланысты сипаттаушы, корреляция коэффициенті. Егерде С=1 болса, онда δΣ – мәні алгебралық жолмен, ал С=0 болса, геометриялық жолмен табылады.
- кездейсоқ шамалардың арасындағы өзара байланысты сипаттаушы, корреляция коэффициенті. Егерде С=1 болса, онда δΣ – мәні алгебралық жолмен, ал С=0 болса, геометриялық жолмен табылады.
Есептеу кездерінде егер Сkj>0,7, болса, онда Сk j мәнін 1-ге теңеп алады да,  мәнін алгебралық жолмен табады. Егер C
мәнін алгебралық жолмен табады. Егер C 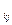 < 0.7,болса, онда Сk j = 0 деп қабылдап, қателік қосындысын
< 0.7,болса, онда Сk j = 0 деп қабылдап, қателік қосындысын  геометриялық жолмен табады.
геометриялық жолмен табады.
Есептеулерді жеңілдету үшін, мәндері аз мөлшерде болып келетін қателіктерді еспке алмайды. Мысалға, екі қателікті қосуды қарастырайық.
 =
= 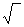

 +
+ 
 , мұндағы
, мұндағы  1 >
1 >  2.
2.
Егерде  2 < 0.05
2 < 0.05 
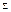 шарты орындалса, онда
шарты орындалса, онда  қателігін ескермесе де болады, яғни
қателігін ескермесе де болады, яғни


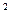
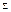 -
- 
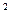 1 =
1 = 
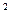 2. Соңғы теңдеуден келесі теңсіздікті алуға болады
2. Соңғы теңдеуден келесі теңсіздікті алуға болады  ; ары қарай
; ары қарай 
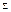 =
=  1 деп ұйғарып алатынымыз
1 деп ұйғарып алатынымыз
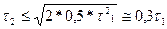
Сонымен, егер бір қателіктің мәні екіншісінен үш есе кем болса, онда ол қателікті ескермеуге болады. Бұдан шығатын салдар, үлгі аспабының өлшеу қателігі жұмыс аспабының өлшеу қателігінен кем дегенде үш есе кем болуы қажет.
Сонымен, қателіктерді қосу ережесін келесі түрде тұжырымдауға болады.
а) қателіктерді систематикалық және кездейсоқ аддитивті және мультипликативті қателіктерге жіктеу. Кездейсоқ қателіктер үшін математикалық күтім орта квадраттық ауытқу және таралым заңдылығын анықтау қажет, соннымен қатар қателіктердің өзара корреляциялық байланысын табу керек.
б) өлшеу құрылғысының систематикалық қателіктерінің қосындысын табу.
в) өлшеу құрылғысы үшін кездейсоқ қателіктерді қосу қажет. Ол үшін кездейсоқ қателіктердің математикалық күтімдерін өзара қосады, алынған қосындыға систематикалық қателікті қосады. Табылған қателікті қателіктің систематикалық бөлігі деп қарастырамыз. Кездейсоқ қателіктердің орта квадраттық ауытқуын және таралым заңдылығын анықтайды.
г) өлшеу құрылғысы қателігінің ∆х берілген сенімділік ықтималдылығы бойынша сенімділік интервалының шекаралық мәндерін келесі теңсіздіктен табу қажет.
М [∆x]-kδ(∆x)<∆x+М [∆x]+kδ(∆x)
Мұндағы М [∆x], δ(∆x) – берілген шамалар, k – қорытқы таралу заңдылығына және сенімділік ықтималдылығының мәніне тәуелді анықталатын коэффициент. Мысалға, егер таралым заңдылығы қалыпты болса, ал сенімділік ықтималдылығы р(-∆хг<х<∆хг)=0,95 тең болса, онда к=2.
Дата добавления: 2015-10-16; просмотров: 838 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| НЕГІЗГІ ТҮСІНІКТЕМЕЛЕР МЕН АНЫҚТАМАЛАР | | | Дәріс бойынша тест сұрақтары |