Энтропия сообщения максимальна, если события равновероятны.

Энтропия всегда неотрицательна.

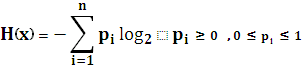
2.Энтропия равна нулю в том крайнем случае, когда вероятность одного из событий равна 1. Это случай, когда о сообщении все известно и результат не приносит никакой информации.

H(p)

1 H₀

0 0,5 p

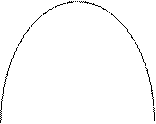
Энтропия сообщения максимальна, если события равновероятны.

Т.е., если , то .

Это свойство определяется в падении информации по Шеннону и по Хартли. В случае неравновероятности событий количество информации по Шеннону всегда меньше потенциальной информативной емкости.

4.Энтропия аддитивна.

Пусть задано два сообщения A= и B= .

C= , A и B являются независимыми и составляют полную группу, т.е.

Кроме аксиом Шеннона, которые использовались для формулировки понятия энтропии, им были использованы специальные подходы. Подходы Шеннона к определению количества информации сообщения длиной L в условиях заданной вероятностной схемы сопровождается специальными требованиями:

1. Пустое сообщение не содержит информации.

=0

2. Количество информации, содержащейся в сообщении, пропорционально его длине.

, то .

Если есть некоторое сообщение T длиной L символов некоторого алфавита А объемом n, то количество информации , где .

Хинчен и Фадеев через задание своих аксиом показали, что энтропия конечной вероятностной схемы однозначно определяется с точностью до постоянного множителя.

, C .

Дата добавления: 2015-10-16