
|
Читайте также: |
Основні формули
Парна регресія
Загальний вигляд формул для обчислення коефіцієнтів 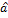 0 і
0 і 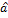 1
1
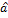 1 =
1 = 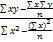
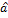 0 =
0 = 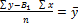 -
- 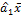
Коефіцієнт детермінації
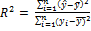 ,
,
Коефіцієнт кореляції


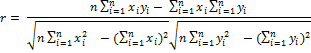
Дисперсія залишків
 ;
;
F-критерія Фішера.

Стандартні похибки оцінок параметрів моделі з урахуванням дисперсії залишків:
 =
= 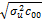
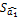 =
= 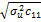
Множинна регресія
Коефіцієнт детермінації

Множинний коефіцієнт кореляції: R = 
F-критерія Фішера:
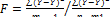
t - критерієм Ст'юдента:
Для перевірки гіпотези про значимість оцінок параметрів моделі (t - критерієм Ст'юдента):
Довірчі інтервали для параметра аj:
Знаходження прогнозних значень змінних
Елементи дисперсійно-коваріаційної матриці:
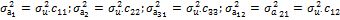 ;
; 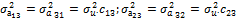
Дисперсія помилок:
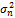 =
= 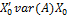
Інтервальний прогноз математичного сподівання М(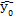 )
)
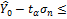 M(
M(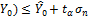
Індивідуальний прогноз індивідуального значення У0:

Дата добавления: 2015-10-16; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Критерій Дарбіна — Уотсона | | | ВАЖНО!!! |