Первичная обработка

На первой стадии «сырые» сведения группируются по тем или иным критериям, заносятся в сводные таблицы, а для наглядного представления данных строятся различные диаграммы и графики. Все эти манипуляции позволяют, во-первых, обнаружить и ликвидировать ошибки, совершенные при фиксации данных, и, во-вторых, выявить и изъять из общего массива нелепые данные, полученные в результате нарушения процедуры обследования, несоблюдения испытуемыми инструкции и т. п. Кроме того, первично обработанные данные, представая в удобной для обозрения форме, дают исследователю в первом приближении представление о характере всей совокупности данных в целом: об их однородности–неоднородности, компактности-разбросанности, четкости–размытости и т. д. Эта информация хорошо читается на наглядных формах представления данных и связана с понятием «распределение данных».

Под распределением данных понимается их разнесенность по категориям выраженности исследуемого качества (признака). Разнесенность по категориям показывает, как часто (или редко) в определенном массиве данных встречаются те или иные показатели изучаемого признака. Поэтому такой вид представления данных называют «распределением частот». Выраженность признака, как видели выше, может быть представлена в оценках: «есть – нет» или «равно – неравно» (номинативные данные), «больше – меньше» (порядковые данные), «настолько-то больше или меньше» (интервальные данные), «во столько-то раз больше или меньше» (пропорциональные данные). Первая категория оценок предполагает явную дискретность выраженности изучаемого признака, остальные – непрерывность (хотя бы теоретически). Проиллюстрируем это примерами.

Пример для дискретных данных

В трехтысячном трудовом коллективе были выбраны сто человек, которые давали ответ на вопрос: «какой цвет вы предпочитаете?». Предлагалось 6 вариантов: белый (Б), черный (Ч), красный (К), синий (С), зеленый (3), желтый (Ж). В данном случае каждый цвет – это самостоятельная категория выраженности признака «окраска». Допустим, цель – выбор дизайнером окраски рабочих помещений, где трудятся эти люди. Итоги опроса, зафиксированные в протоколе, подсчитали и занесли в таблицу 1 (табулировали).

Таблица 1

Итоги опроса

Цвет	Количество выборов
Абсолютная частота	Относительная частота	%
Б		0,08
Ч		0,06
К		0,21
С		0,20
З		0,34
Ж		0,11
Сумма		1,00

Частота (абсолютная частота) – это число ответов данной категории в выборке, частость (относительная частота) – это отношение частоты ко всей выборке. Под выборкой понимается все множество полученных в исследовании значений изучаемого признака (свойства, качества, состояния) объекта. В нашем примере выборка равна 100. Понятие выборки связано с понятием генеральной совокупности (или популяции), которая представляет собой все возможное множество значений изучаемого признака. В нашем примере она равна 3000. Поскольку даже ограниченные популяции обычно весьма велики, то опыты проводятся только на выборках. Поэтому встает вопрос о репрезентативности выборки, т. е. о том, можно ли результаты, полученные на выборке, переносить на всю совокупность. Для этого привлекают статистические методы доказательства репрезентативности. Таким образом, выборка есть часть генеральной совокупности. Краткое описание этих множеств производится с помощью так называемых описательных мер (мер центральной тенденции, разброса и связи), вычисление которых производится при вторичной обработке данных. Значения мер, вычисленные для генеральных совокупностей, называются параметрами, для выборок – статистиками. Параметр описывает генеральную совокупность также, как статистика – выборку. Принято обозначать статистики латинскими буквами, а параметры – греческими. Правда, в психологических исследованиях этих правил не всегда строго придерживаются.

На основании табличных данных можно построить диаграмму, где распределение представлено нагляднее:

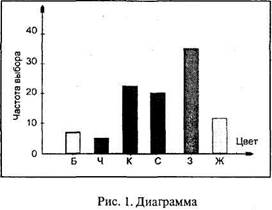
Пример для непрерывных данных

Данные непрерывного характера можно представить веще более наглядной форме: в виде гистограмм, полигонов икривых.

В опытах В. К. Гайды, описанных в учебном пособии для студентов-психологов [76, с. 23-25], участвовало 96 испытуемых. Определялся цвет последовательного образа восприятия насыщенного красного цвета. С этой целью каждый испытуемый в течение одной минуты рассматривал окрашенный в красный цвет образец, а затем переносил взгляд на белый экран, где видел круг в дополнительных цветах. Рядом с ним находился цветовой круг с разноокрашенными секторами, на котором испытуемый должен был выбрать тот цвет, который соответствовал цвету возникшего у него последовательного образа. При этом испытуемый не называл цвет, а лишь его номер в цветовом круге. Цветовой круг нормирован таким образом, что соседние цвета отличаются в нем друг от друга на одинаково замечаемую величину. Следовательно, цветовой круг можно рассматривать как интервальную шкалу. Наряду с этим цветовой круг характеризуется и еще одним свойством. В частности, можно себе представить, что между двумя соседними цветами, например между зеленовато-голубым и голубовато-зеленым, имеется еще множество не замечаемых человеческим глазом цветовых переходов. В этом смысле цветовой круг представляет собой пример непрерывной переменной. Фактически же испытуемые всегда выделяют конечное число цветовых оттенков и поэтому свой выбор останавливают на конкретном номере (или названии) цвета. В рассматриваемом эксперименте испытуемые определяли свой последовательный образ в диапазоне от № 16 – зеленовато-голубой цвет до № 23 – желтовато-зеленый. Полученные данные можно табулировать, что и сделано в таблице 2.

Таблица 2

Последовательный образ	Частота выбора цвета образа
Σ

Как видно, в построении таблиц 1 и 2 нет принципиального различия. Но разница в характере первичных данных, отображенных в обеих таблицах, все же есть, и она обнаруживается при их графическом изображении. В самом деле, рис. 2 представляет собой уже не столбиковую, а ступенчатую диаграмму, называемую гистограммой. Следует обратить внимание на то, что все участки (столбики) ступенчатой диаграммы расположены вплотную друг к другу (числовые переменные на оси абсцисс гистограммы пишут против центральной оси каждого участка).

От гистограммы легко перейти к построению частотного полигона распределения, а от последнего – к кривой распределения. Частотный полигон строят, соединяя прямыми отрезками верхние точки центральных осей всех участков ступенчатой диаграммы (рис. 3). Если же вершины участков соединить с помощью плавных кривых линий, то получится кривая распределения первичных результатов (рис. 4).

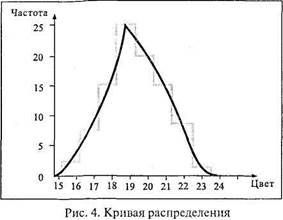
Переход от гистограммы к кривой распределения позволяет путем интерполяции находить те величины исследуемой переменной, которые в опыте не были получены.

Дата добавления: 2015-10-21