Элементы рентгеноструктурного анализа

В рентгеноструктурном анализе используется внесистемная единица длины - ангстрем (Å). (1 Å = 1∙10^-10 м). Основная формула рентгеност­руктурного анализа (формула Брэггов-Вульфа) представляет собой условие дифракционных максимумов при дифракции рентгеновских лучей на кристал­лической решетке вещества и связывает углы дифракции с межплоскостными расстояниями и длиной волны рентгеновского излучения

2d× Sinθ = n·λ, (1)

где d - межплоскостное расстояние, Å,

θ - угол дифракции, отсчитываемый от атомных плоскостей, град.,

λ - длина волны рентгеновского излучения, Å,

n - порядок дифракционного максимума (обычно n = 1).

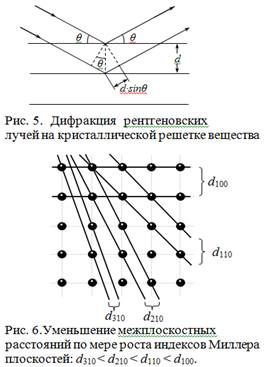
Рис. 5 иллюстри­рует формулу Брэггов-Вульфа. Рентгеновские волны, отражаясь от со­седних кристаллогра­фических плоскостей, дают интерференцион­ный максимум, если разность хода Δ для лу­чей составляет целое число длин волн Δ = nλ.

Из геометрических сооб­ражений следует, что разность хода

Δ = 2d · Sinθ (рент­геновские лучи не ис­пытывают преломления в среде, поэтому для них оптическая раз­ность хода равна гео­метрической). Объеди­няя (2) и (3), получим формулу Брэггов-Вульфа (1). Следует учесть, что отражающие плоскости не имеют ничего общего с плоскими поверхностями, ограничивающими дан­ный образец.

Некоторые системы отражающих плоскостей в простой кубической решетке приведены на рис. 6.

Таблица 1 – Углы гониометра и сцинтилляционного счётчика

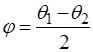для монокристаллического кремния а_Si = 0,5431 нм (5,431)

Заданная кристаллографическая плоскость	Материал анода
Cr λ K α =2,2896 Ǻ	Cu λ K α = 1,5405 Ǻ	Mo λ K α = 0,7093 Ǻ
Гониометр	Счётчик	Гониометр	Счётчик	Гониометр	Счётчик
(111) (100)	21,41˚ 57,47 ˚	42,82˚ 114,95˚	14,26˚ 34,56 ˚	28,53˚ 69,12 ˚	6,49˚ 15,14˚	12,99˚ 30,28˚

Дата добавления: 2015-10-21