Практическая часть

Задача 1.1

В закрытом резервуаре налита вода. Определить высоту 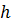поднятия ртути в дифманометре и высоту 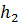поднятия воды в закрытом пьезометре, если показание пружинного манометра, подключенного на уровне точки А, равно 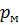(рисунок 1.1). Атмосферное давление считать нормальным, глубина погружения точки А равна 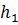. Плотность ртути 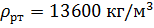, воды .

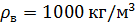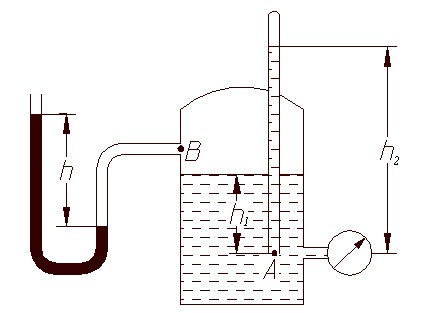
Рисунок 1.1

Таблица исходных данных:

Высота, м	Манометрическое давление в точке А на глубине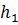

Решение:

Находим давление в точке А:

Отсюда находим давление :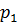

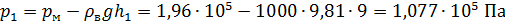
Найдем высоту 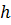поднятия ртути в дифманометре из уравнения:

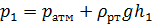
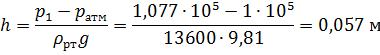
Определяем высоту 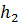поднятия воды в закрытом пьезометре из уравнения:

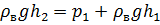
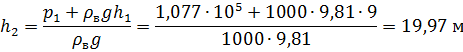
Ответ:

Задача 1.3

В цилиндрическом сосуде диаметром и высотой налита вода с начальным уровнем 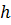(рисунок 1.3). Определить:

1) Будет ли выплескиваться вода, если сосуд будет вращаться с постоянной частотой вращения ?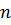

2) На каком расстоянии 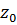от дна будет находиться самая низшая точка свободной поверхности?

3) С какой частотой нужно вращать сосуд, чтобы вода поднялась до краев сосуда?

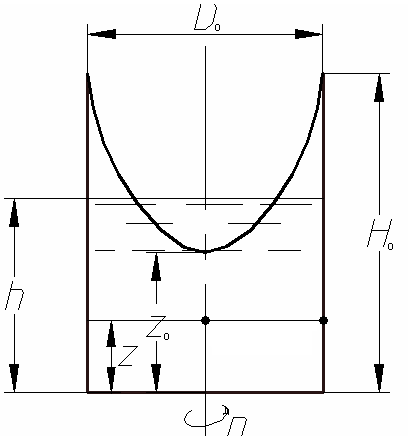
Рисунок 1.3

Таблица исходных данных:

Высота, м	Диаметр, м	Частота вращения, мин^-1

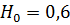
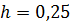
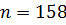
Решение:

Определяем угловую скорость:

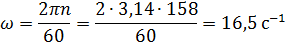
Определяем наибольшую разницу уровней между наинизшей точкой свободной поверхности в центре и наивысшей у боковой стенке:

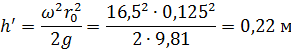
Наибольшее понижение свободной поверхности на оси вращения по сравнению с первоначальным уровнем воды в сосуде равно:

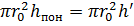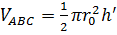Из равенства объемов следует: объем жидкости - объем параболоида . Так как , то

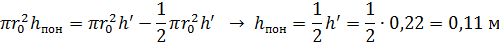
Наибольшее повышение уровня у боковых стенок над первоначальным уровнем воды в сосуде:

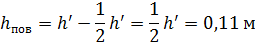
Наиболее пониженная точка свободной поверхности В находится от дна на расстоянии:

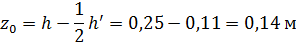
По отношению ко дну точка С как самая высокая точка свободной поверхности находится на расстоянии:

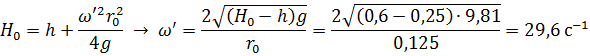
Для того, чтобы вода поднялась до краев сосуда, необходимо вращать сосуд с частотой:

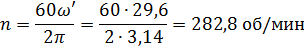
Имеем 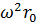- центробежное ускорение у стенки. Для того, чтобы вода не выплескивалась при вращении сосуда с постоянной данной в условии частотой вращения, необходимо, чтобы выполнялось условие:

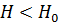
Т.к.

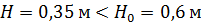
Вода выплескиваться не будет.

Ответ: 1) не будет; 2) 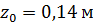; 3)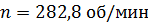

Задача 1.5

Треугольное отверстие АВС в вертикальной стенке закрытого резервуара, представляющее равносторонний треугольник, закрыто щитом (рисунок 1.5). Определить равнодействующую силу гидростатического давления бензина на щит и точку ее приложения, если заданы линейные размеры: 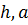и манометрическое давление 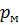на свободной поверхности бензина.

Рисунок 1.5

Таблица исходных данных:

Линейные величины, м	Манометрическое давление, атм

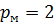
Решение:

Гидростатическое давление изменяется по закону:

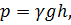
где .

Избыточное гидростатическое давление на АВ с учетом 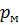будет равно:

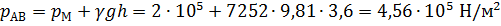
Давление в точке С равно:

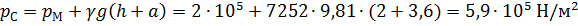
Среднее значение гидростатического давления равно:

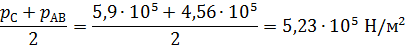
Площадь треугольника АВС:

Равнодействующее гидростатическое давление равно:

где 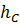- центр тяжести треугольника под нижней свободной поверхностью жидкости. Как известно центр тяжести равностороннего треугольника лежит на расстоянии 1/3 высоты треугольника, т.е.

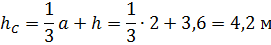
Определяем равнодействующую силу гидростатическое давление бензина на щит и точку ее приложения:

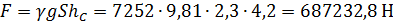
В нашем случае центр давления совпадает с центром тяжести равностороннего треугольника.

Ответ: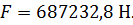

Задача 1.7

Под каким давлением 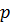(рисунок 1.7) нужно подать жидкость в безштоковую полость гидроцилиндра, чтобы поршень начал двигаться вправо, преодолевая силу 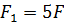на штоке, если давление в штоковой полости 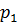? На какую силу сжатия 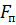нужно отрегулировать пружину предохранительного клапана, чтобы он открывался при возрастании силы на штоке до величины 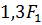, если диаметр входного отверстия (седла) клапана 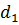, а давление 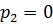. Силы трения не учитывать.

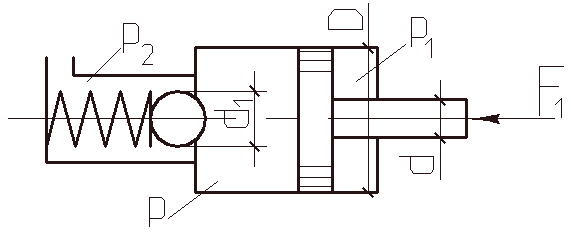
Рисунок 1.7

Таблица исходных данных:

Диаметр, мм	Давление, МПа	Сила, Н

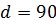
Решение:

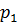1) Для движения штока необходимо, чтобы сила давления в бесштоковой полости равна +сила давления от . Таким образом:

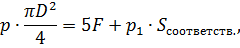
где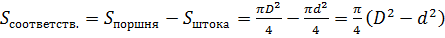

Следовательно,

Отсюда выражаем давление, под которым нужно падать жидкость в бесштоковую полость гидроцилиндра, чтобы поршень начал двигаться вправо:

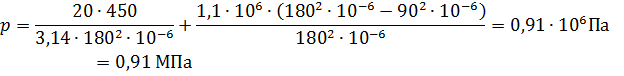
2) При силе на штоке в

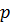в бесштоковой полости:

Для открытия клапана необходимо равенство сил слева и справа от него:

Определяем силу сжатия 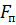, на которую нужно отрегулировать пружину предохранительного клапана, чтобы он отрывался при возрастании силы на штоке до величины :

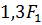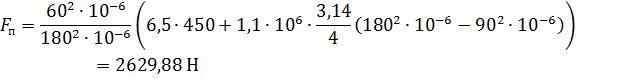
Ответ:

Задача 1.9

Определить осадку 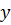и проверить остойчивость плавания в воде деревянного бруса (рисунок 1.9). Размеры бруса: высота 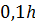, ширина , длина 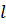. Относительная плотность бруса 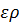. Вычислить наименьшую высоту , при которой брус будет еще остойчив.

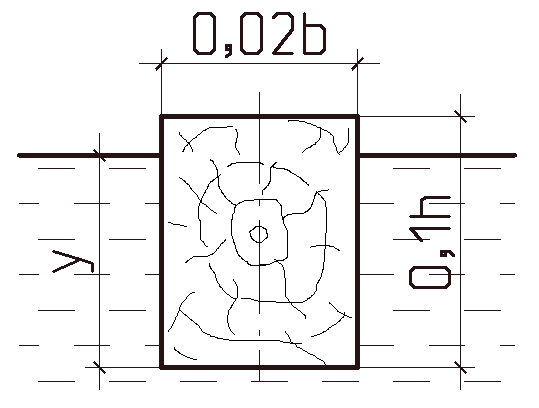
Рисунок 1.9

Таблица исходных данных:

Относительная плотность	Плотность воды, кг/м^3	Длина, м	Ширина, м	Высота, м

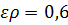
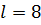
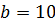
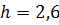
Решение:

Для определения осадки бруса записываем условие плавания:

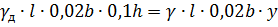
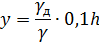
Относительная плотность бруса:

Поскольку брус – однородное прямоугольное тело, его центр тяжести (т.С) находится на середине высоты 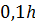. Центр водоизмещения (т. D) лежит в центре тяжести объема погруженной части , т.е. на высоте от нижней кромки бруса. Т.к. т.С выше т.D на величину:

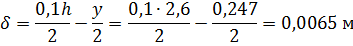
Для проверки остойчивости тела необходимо вычислить величину метацентричного радиуса .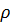

Находим центральный момент инерции плоскости ватерлинии относительно продольной оси:

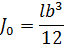
Тогда по формуле:

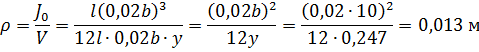
Т.к. 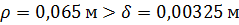, то брус остойчив.

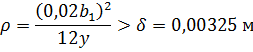
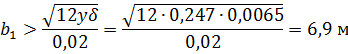
Ответ:

Задача 1.11

В вертикальной стенке, разделяющей резервуар на две части, расположено круглое отверстие с диаметром 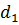и насадкам длиной 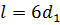(рисунок 1.11). В наружной стенке имеется другое отверстие диаметром 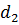. Центры обоих отверстий расположены на высоте 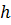от дна. Уровень воды в левой части резервуара 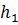, расход через отверстия 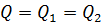. Определить уровень 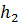воды в правой части резервуара и диаметр 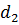отверстия в наружной стенке.

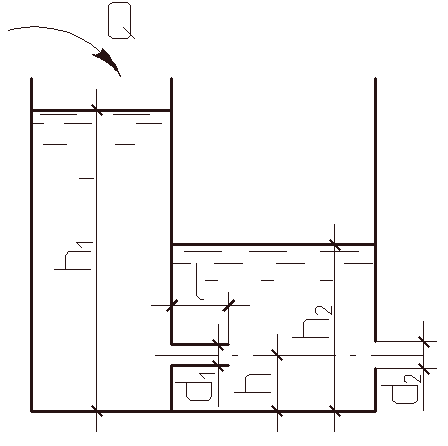
Рисунок 1.11

Таблица исходных данных:

Параметр	Расход, л/с	Вид насадка
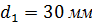
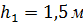
		Внешний цилиндрический

Решение:

Осредненные значения коэффициентов для режима истечения жидкости через внешний цилиндрический насадок для маловязких жидкостей (в нашем случае вода) следующие:

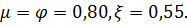
Коэффициент сжатия находим из соотношения:

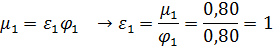
Запишем уравнение расхода :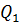

Из этого уравнения находим скорость истечения в сжатом сечении струи:

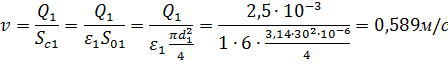
Определяем расчетный напор:

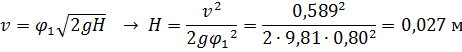
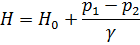
Так как 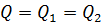, то и . Тогда:

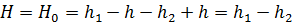
Отсюда находим уровень воды в правой части резервуара:

Запишем уравнение расхода :

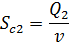
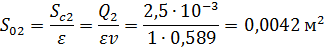
Ответ: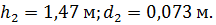

Задача 1.13

Центробежный насос подает воду температурой в систему (рисунок 1.13). Расход воды составляет 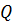. Всасывающая труба насоса диаметром , общей длиной 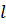имеет два поворота под углом 90° и приемный клапан, коэффициент сопротивления которого . Определить максимально возможную высоту установки оси насоса 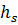над уровнем воды в отстойнике, исходя из условия, что давление воды при входе в насос должно быть на 0,02МПа выше давления парообразования, равного 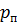. Абсолютное давление на свободной поверхности жидкости вотстойнике принять равным 0,1 МПа. Эквивалентная шероховатость поверхности трубы , плотность воды .

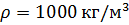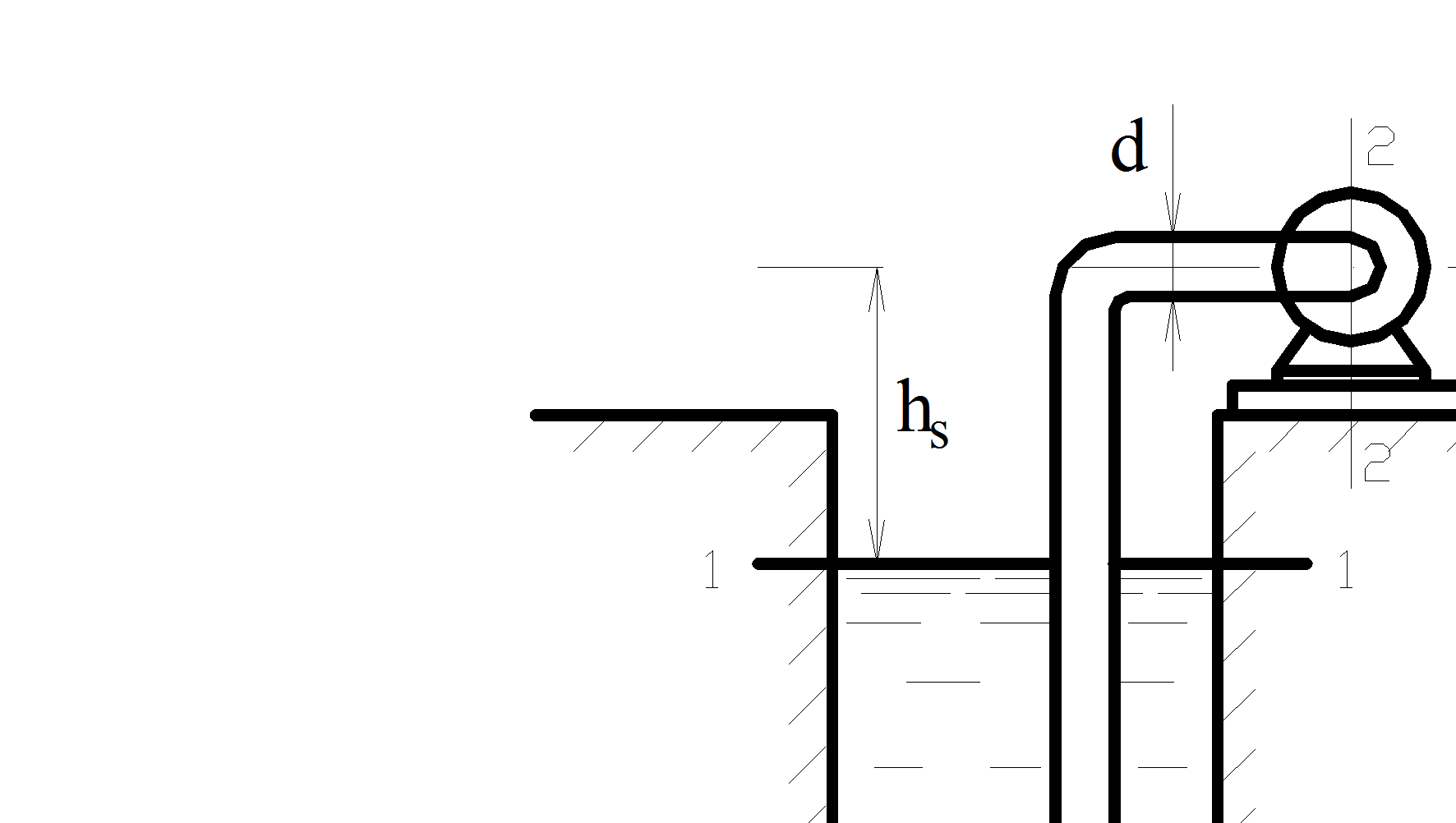
Рисунок 1.13

Исходные данные: С.

Решение:

Запишем уравнение Бернулли для всех сечений:

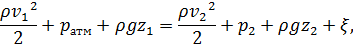
где 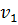- средняя скорость течения воды на свободной поверхности водоема; - атмосферное давление; - средняя скорость течения воды во всасывающей трубе; - потери давления.

Высота расположения оси насоса над уровнем воды отстойника:

При 30°С: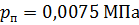

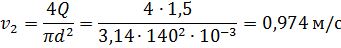
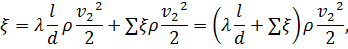
где .

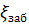
Число Рейнольдса:

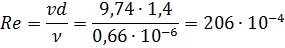
Коэффициент гидравлического сопротивления:

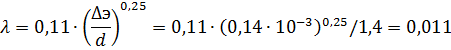
Коэффициент сопротивления на поворот:

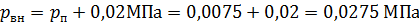
Максимальная высота расположения оси насоса над уровнем воды отстойника:

Ответ: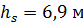

Список использованной литературы

1. Б.Б. Некрасов «Гидравлика и ее применение на летательных аппаратах». Издательство «Машиностроение»: Москва – 1967.

2. А.В. Андреевская, Н.Н. Кременецкий, М.В. Панова «Задачник по гидравлике». «Энергия»: Москва 1970.

3. Конспект лекций по дисциплине «Гидравлика».

4. Т.М. Башта, С.С. Руднев, Б.Б. Некрасов, О.В. Байбаков, Ю.Л. Кирилловский «Гидравлика, гидравлические машины и гидравлические приводы». Издательство «Машиностроение»: Москва, 1970.

5. А.Д. Альтшуль, П.Г. Киселев «Гидравлика и аэродинамика». Издательство литературы по строительству: Москва – 1965.

6. В.Н. Метревели «Сборник задач по курсу гидравлика» - М.: Высш. шк., 2008. – 192 с.

7. С.И. Часс «Гидромеханика в примерах и задачах»: Учебное пособие. – Екатеринбург: Изд-во УГГУ, 2006, 216с.

Дата добавления: 2015-10-21