Оптические фононы

Наряду с акустическими волнами и соответствующими им акустическими фононами, в кристаллах, состоящих из атомов разного сорта (например, из атомов различной массы), существует ещё один тип коллективных возбуждений, при котором соседние атомы независимо от длины волны колеблются в противофазе. Они также существуют в кристаллах, состоящих из атомов одного сорта, но имеющих несколько атомов в элементарной ячейке. Эти моды колебаний для цепочки, состоящей из атомов двух сортов, показаны на рис. 5.6.1.

Рис. 5.6.1. Возможные поперечные колебания цепочки (а), состоящей из

двух сортов атомов: 6) акустические колебания с длиной волны λ = 8а;

в, г) оптические колебания с длиной волны λ = 8а и 8а < λ < 9а;

д) преобразование акустических колебаний с минимальной длиной волны

в оптические с максимальной длиной волны

Вертикальные пунктирные линии показывают положения атомов одного сорта. Впервые такой тип колебаний был обнаружен в ионных кристаллах (таких, как NaCI, KBr) при воздействии на кристалл световой волны, вследствие чего он получил название оптических колебаний. Таким образом, в кристаллах, где возможны оптические колебания, одному и тому же значению волнового вектора соответствуют две волны с одной

и той же поляризацией: акустическая и оптическая.

Поляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.

Причиной возникновения поляризации волн может быть:

· несимметричная генерация волн в источнике возмущения;

· анизотропность среды распространения волн;

· преломление и отражение на границе двух сред.

Оптические колебания, как и акустические, квантуются. Кванты энергии оптических колебаний называются оптическими фононами. Характерной особенностью оптических колебаний является то, что во всех оптических модах, независимо от длины волны, соседние атомы колеблются практически в противофазе и поэтому частоты оптических фононов близки к значению предельной частоты акустических фононов и слабо зависят от величины волнового вектора.

В общем случае в трёхмерных решётках возможны три типа акустических колебаний: продольные и два типа поперечных и, соответственно, три типа оптических. Таким образом, спектр колебаний кристаллической решётки при каждом заданном волновом вектора k описывается шестью ветвями: тремя акустическими и тремя оптическими.

§ 5.7. Локальные и квазилокальные фононы (Брандт, Кульбачинский)

Этот тип фононов связан с присутствием в решётке примесных атомов, с массой, существенно отличающейся от массы атомов, образующих решётку. Примесные атомы совершают сложные колебательные движения, квантами, энергии которых и являются локальные или квазилокальные фононы. В общем случае возмущение, которое вносит примесный атом, зависит от его массы, величины силовых постоянных, связывающих примесный атом с окружающими атомами кристалла, и положения примесного атома в решётке. Расчёт этого возмущения представляет собой сложную и, в известной степени, неопределённую задачу, так как для её решения необходима точная информация о величине и анизотропии силовых постоянных в первой и, по крайней мере, второй координационных сферах, окружающих примесный атом, а также о его местонахождении в решётке.

Чтобы исключить неопределённость в положении примесных атомов,

Будем считать, что они замещают собственные атомы кристалла. Для металлов с чисто металлическим характером связи можно предположить, что силовые постоянные должны зависеть от радиуса и анизотропии внутренних электронных оболочек nримесного иона и его валентности. Однако, эти изменения обычно невелики, и для того, чтобы выяснить физическую картину колебаний примесных атомов, учитывать их не будем.

Итак, пусть примесный атом с массой M * находится в одном из узлов решётки и взаимодействует с окружающими атомами, имеющими массу m, так же как атомы матрицы между собой. Очевидно, в этой модели, при равенстве массы nримесного атома и атомов матрицы, фононный спектр вообще не изменяется. Если же М * ≠ m, то спектр изменяется, причём здесь существует два физически различных случая: М * < m М * > m. Рассмотрим случай М * < m.

Решим задачу о колебаниях цепочки атомов с периодом а, в которой один атом замещён на примесный. Посмотрим, чем эта задача отличается от задачи о колебаниях цепочки, состоящей из атомов двух сортов. Цепочка из атомов двух сортов была однородна, и можно было выбрать любые два разнородных атома и записать для них уравнения движения. Как следствие этого, решение не зависело от номера атома. Теперь ситуация другая. Примесный атом вносит локальное возмущение в колебания цепочки. Поскольку масса М * примесного атома меньше массы m атомов цепочки, а силовые постоянные везде одни и те же, естественно предположить, что предельная частота колебаний примесного атома превышает предельную частоту колебаний в цепочке, образованной только атомами с массой m, и равную при (см. рис. 5.2.3)

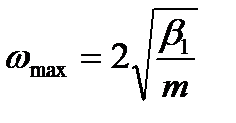(5. 7. 1)

В нашем случае , где , а - расстояние между ядрами в решетке. Тогда получим что согласуется с оценками Киржница (хотя у Киржница есть описка: стоит степень 1/3 а должно быть 1/2).

Обозначим координату nримесного атома 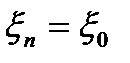, силовую постоянную, как и раньше, через 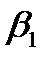и будем учитывать только взаимодействие с ближайшими соседями.

По аналогии с (5.2.4) запишем уравнение движения для примесного атома в виде

(5.7.2)

Для соседнего атома

(5.7.3)

Для следующего атома

(5.7.4)

и т.д.

Обозначим через

Очевидно, что для атомов с номерами -1 и -2 уравнения будут идентичны уравнениям (5.7.3) и (5.7.4). Для однородной цепочки решение искалось в виде бегущей волны. Здесь же будем искать решение для колебаний с частотой в форме экспоненциально затухающей по мере удаления от примесного атома (n = 0) функции

, (5.7.5)

считая, что собственная частота колебаний атомов m равна предельной частоте колебаний атомов в цепочке. Множитель (- 1)ⁿ учитывает, что в зарезонансной области частот соседние атомы колеблются в противофазе,

α - коэффициент, определяющий скорость затухания колебаний при удалении от атома с номером n = 0.

Локальные колебания характеризуются двумя параметрами: и α, которые и подлежат определению. Подставляя (5.7.5) в (5.7.2), находим

(5. 7.6)

Подстановка (5.7.5) в уравнения (5.7.3) и (5.7.4) даёт один и тот же результат:

(5.7.7)

Уравнения (5.7.6) и (5.7.7) совместимы при условии

, (5.7.8)

Откуда имеем

(5.7.9)

Легко заметить, что при , . При

(5.7. 1 0)

Но это соотношение означает, что примесный атом в цепочке колеблется так, как если бы соседние с ним атомы были неподвижны, т. е. частота колебаний примесного атома равна частоте парциальных колебаний атома с массой в цепочке с силовой постоянной .

Посмотрим, как при уменьшении массы примесного атома изменяется область, в которой локализуются колебания с частотой . Ширина этой области определяется множителем exp(-α|n|a). Амплитуды высокочастотных колебаний убывают при удалении от примесного атома (при росте n) по закону (см. (5.7.8))

(5.7. 1 1)

При М* = 0,5 m амплитуда колебаний соседнего атома в три раза меньше амплитуды ξ, следующего - в 9 раз, и т.д.

Обратим внимание, что при амплитуда перестаёт зависеть от n.

Таким образом, лёгкий примесный атом в решётке колеблется с частотой, превышающей предельную частоту акустических колебаний (а в кристаллах с несколькими атомами в элементарной ячейке - и оптических).

Высокочастотные колебания локализуются в очень малом объёме кристалла. Их амплитуда быстро затухает при удалении от лёгкого атома. Поскольку в решётке не существует коллективных возбуждений (акустических и оптических) такой частоты, примесный атом колеблется практически индивидуально, слабо возмущая, с одной стороны, колебания соседних атомов в решётке, а с другой - слабо изменяя частоту собственных колебаний в результате связи с ними. При этом разность фаз между колебаниями примесного атома и его соседей непрерывно изменяется.

Колебания примесного атома квантуются:

, n = 0, 1, 2,..., (5.7. 1 2)

что позволяет говорить о локальных фононах с энергией · Колебаниям

лёгких примесных атомов в решётке соответствует в спектре плотности фононных состояний очень узкий по частоте пик, расположенный правее предельной фононной частоты. Заметим, что примесный высокочастотный пик в плотности фононных состояний может возникнуть даже в том случае, если масса примесного атома близка к массе атомов матрицы, но силовые постоянные, связывающие примесный атом с соседними, по какой либо причине сильно увеличены.

5.7. Локальные фононные моды http://dssp.petrsu.ru/p/tutorial/ftt/Part5/part5_7.htm

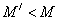Фононный спектр кристалла может изменяться в присутствии дефектов решетки и примесных атомов. Заменим атом цепочки, находящийся в начале координат, более легким атомом. Тогда под влиянием колебаний этого атома близлежащие атомы будут колебаться несколько иначе, нежели атомы, расположенные вдали от него [69]. Пусть масса «дефектного» атома , а всех остальных − M ( ). Покажем, что одно из нормальных колебаний решетки локализуется в районе более легкого атома и соответствующая частота увеличивается по сравнению с максимальной частотой колебаний ненарушенной (исходной) решетки. Учтем взаимодействие только ближайших соседних атомов и предположим, что оно одинаково для всех сортов атомов, а примесный атом находится в нулевом положении в цепи. Тогда уравнения движения атомов решетки будут иметь вид

(5.66)

Поскольку при удалении от примесного атома деформация затухает, то решение будем искать в виде «затухающей» функции, которая в пределе приближается к форме нормального колебания максимальной частоты для решетки без дефекта. Нумеруя координату атома символом n, получим решение у границы зоны Бриллюэна для невозмущенного колебания в виде

.

(5.67)

В случае наличия дефекта и появления возмущенного состояния решение будет иметь вид

,

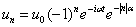(5.68)

где a − коэффициент, который должен быть определен. Подставляя (5.68) в (5.66), получим

(5.69)

и в то же время

.

(5.70)

Поскольку волны в цепочке объединяют колебания всех атомов, то можно приравнять (5.69) к (5.70). В результате получим

.

(5.71)

Учитывая, что максимальная частота колебаний для невозмущенной решетки, в которой , определяется как , получим

.

(5.72)

Этот результат свидетельствует о том, что частоты колебаний при наличии дефекта могут оказаться в области запрещенных частот. Это приводит к дополнительным частотам в фононном спектре, а значит и дополнительным энергиям мод колебаний. Например, это наблюдается при замене в кристалле KCl иона хлора Cl^- на ион иода I^-.

Определенные виды примесей, особенно очень тяжелые, могут приводить к локализованным колебаниям, чьи частоты лежат в области разрешенных фононных частот чистого исходного кристалла. Такие колебания характеризуются сильно увеличивающейся амплитудой колебания примесного атома, т. е. возникает резонансное квази-локализованное состояние. Этот эффект наблюдается, например, когда ион Ag⁺ замещает ион K⁺ в кристалле KI.

Рассмотренные нами локализованные состояния называются локальными фононными модами.

Рис. 2. Схематический вид функции распределения частот акустических и оптических ветвей; - частоты особенностей Ван Хова, и - частоты локального и квазилокального колебаний.

Наряду с локальными колебаниями могут существовать т. н. квазилокальные колебания, к-рые охватывают весь кристалл, но при к-рых амплитуда колебаний дефекта значительно превосходит амплитуду колебаний атомов в объёме. Частоты таких колебаний попадают в полосы частот идеального кристалла и обычно оказываются расположенными вблизи краёв этих полос. Плотность колебаний имеет узкий резонансный пик на квазилокальной частоте (рис. 3).

Качественно отличная ситуация имеет место при рассмотрении колебаний тяжёлых примесных атомов, масса которых 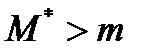. Дело заключается в том, что парциальная частота колебаний тяжёлого атома лежит в области разрешённых фононных частот. Поэтому взаимодействие примесных колебаний с колебаниями решётки в общем случае является достаточно сложным. Задача несколько упрощается для очень тяжёлых примесей в пределе . В этом случае примесный атом можно рассматривать как осциллятор с собственной частотой, близкой к · На этот осциллятор действует спектр возбуждающих сил с частотами, соответствующими области фононных частот от до · Очевидно, из всей области фононных частот примесный атом наиболее эффективно (резонансно) взаимодействует только с модами колебаний, имеющими частоты, близкие к · Остальные моды оказывают слабое воздействие на его колебания. Обратим внимание, что резонансное возбуждение колебаний примесного атома происходит под действием продольных и поперечных мод (в трёхмерном случае), имеющих одну и ту же частоту , но разные длины волн.

Известно, что амплитуда колебаний осциллятора под действием вынуждающей силы при резонансе пропорциональна корню квадратному из его массы. Поэтому амплитуда колебаний примесного тяжёлого атома в решётке превышает амплитуду фононных мод той же частоты приблизительно в раз, что позволяет говорить о квази-локализованных резонансных колебаниях тяжёлых атомов в решётке.

Подчеркнём, что большая амплитуда колебаний примесного атома соответствует уровню теплового возбуждения колебаний решётки при данной температуре и связана только с большей массой примеси. Сдвиг фаз между колебаниями примесного атома и соседних атомов, колеблющихся с частотой , должен быть близок (как при резонансе под действием возбуждающей силы) к - π/2.

Усиление амплитуды колебаний в некотором интервале частот вблизи

приводит к появлению на кривой спектральной плотности фононных состояний размытого максимума, накладывающегося на монотонную зависимость D(w) в области низких частот. Поэтому такие колебания принято называть квазилокальными в отличие от чисто локальных колебаний, наблюдающихся при . Кванты энергии квазилокальных колебаний можно рассматривать как квазилокальные фононы, локализованные в определённом частотном интервале, но способные перемещаться в решётке, если концентрация примесей достаточно велика и области, в которых тяжёлые атомы возмущают колебания решётки, перекрываются. Таким образом, квазилокальные фононы можно характеризовать своим законом дисперсии и значениями квазиимпульсов. Качественно их можно рассматривать как некоторый низкочастотный аналог оптических фононов.

Отметим ещё одну общую черту квазилокальных колебаний. Различие в амплитуде и фазе колебаний примесных атомов и окружающих их атомов решётки, а также изменение силовых постоянных, связывающих примесный атом с соседями, приводят к нарушению симметрии сил взаимодействия соседних атомов в направлении к примесному атому и в противоположном. Нарушение симметрии может приводить к возникновению сильного ангармонизма колебаний окружающих примесь атомов в радиальном направлении, который быстро затухает при удалении от центра. Таким образом, вокруг каждого примесного тяжёлого атома в решётке образуется область с усиленным ангармонизмом колебаний атомов, охватывающая 2-3 координационные сферы.

---

Дата добавления: 2015-10-21