Взаимодействие фононов

5.8.1. Анrармонизм колебаний атомов. Основной причиной, вызывающей

рассеяние фононов на фононах, является ангармонизм колебаний атомов или ионов в кристаллической решётке. До сих пор колебания решётки рассматривались в гармоническом приближении, т. е. предполагалось, что потенциальная энергия взаимодействия атомов в кристалле (рис. 5.8.1, а) является квадратичной функцией смещения атомов из положения равновесия.

Характерной особенностью колебаний атомов в параболической потенциальной яме, где энергия U квадратично зависит от смещения ξ,

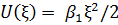, (5.8. 1)

является сохранение симметрии колебаний относительно положения равновесия при увеличении амплитуды колебаний (при переходе осциллятора на более высокие уровни энергии). Поэтому возбуждение осциллятора в гармоническом приближении не приводит к изменению среднего по времени положения атома относительно точки равновесия r = r₀. Это означает отсутствие теплового расширения тела. Соответственно силы 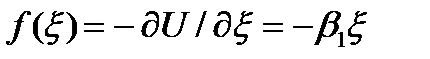, возникающие при смещении атома из положения равновесия, имеют одну и ту же величину независимо от того, смещается ли атом в направлении к ближайшему соседу (т. е. расстояние между атомами уменьшается) или удаляется от него. В результате, силовые постоянные не зависят от объёма кристалла (внешнего давления) и температуры. Кроме того, монохроматические волны не взаимодействуют между собой и, следовательно, монохроматические фононы не рассеиваются друг на друге.

Рис. 5.8. 1. Зависимость потенциальной энергии и взаимодействия атомов от расстояния r между ними. Квадратичная зависимость (а) и несимметричная зависимость (б), r_o - расстояние до положения равновесия при разных температурах Т₁, Т₂, Т₃. которым соответствуют энергии Е_Ti

В действительности колебания решётки не являются гармоническими. Физическая причина ангармонизма заключается в асимметрии сил, действующих на атом при его смещении из положения равновесия.

Рассмотрим какой-либо атом в одномерной цепочке. Сместим атом из положения равновесия по направлению к соседу слева. При этом расстояние между выбранным атомом и соседом слева уменьшится, а расстояние до соседа справа увеличится. В результате нелинейности сил взаимодействия на смещённый атом со стороны левого соседа будет действовать большая сила, чем со стороны соседа справа, хотя обе силы стремятся вернуть атом в положение равновесия. То же происходит и при тепловых колебаниях атомов, при которых расстояния между атомами в решётке изменяются нерегулярным образом: в любой момент времени каждый атом оказывается ближе к какому-то одному из своих соседей, чем к другим, и возникающие силы отталкивания всегда превышают силы притяжения. Такая асимметрия сил взаимодействия означает, что в выражение для потенциальной энергии

взаимодействия U входят члены, содержащие смещение ξ в степени большей, чем вторая.

Зависимость потенциальной энергии от расстояния между атомами r показана на рис. 5.8.1,б. Энергия U возрастает при сближении атомов быстрее, чем по параболическому закону (пунктир), а при их удалении друг от друга - медленнее. Такой характер отклонения U(ξ) описывается поправкой, пропорциональной ξ³:

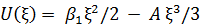, (5.8.2)

(А > 0 - коэффициент ангармонизма). В результате нелинейности сил взаимодействия по ξ силовые постоянные в решётке и частоты колебаний атомов зависят от их амплитуды, а следовательно, и от температуры. Ангармонизм колебаний определяет фонон-фононное взаимодействие, тепловое расширение тела, зависимость упругих постоянных от давления и температуры.

5.8.2. Механизм фонон-фононного рассеяния. Механизм фонон-фононного рассеяния заключается в следующем. Рассмотрим бегущую звуковую волну с волновым вектором q. Волна создаёт в кристалле области сжатия и разряжения. В результате ангармоничности колебаний (нелинейности сил взаимодействия между атомами) коэффициент сжимаемости решётки зависит от объёма. Поэтому волна нарушает однородность среды: её можно рассматривать как движущуюся дифракционную решётку, образованную чередующимися областями с различной сжимаемостью (показателем преломления), на которой рассеиваются другие волны. Таким образом, рассеяние фононов является следствием интерференции звуковых волн, вызванной нелинейностью сил связи в решётке.

В процессе взаимодействия волны обмениваются энергией: две волны могут породить третью более высокой частоты, одна волна может распасться на две с более низкими частотами; две волны могут перейти в две с другими частотами и волновыми векторами и тому подобное. Этот процесс может быть описан как рассеяние фононов друг на друге. В результате взаимодействия двух фононов с частотами w₁ и w₂ возникает третий фонон с частотой w₃, равной w₁ + w₂. Возникновение третьего фонона происходит в соответствии с законами сохранения энергии и импульса. Трёх фононные процессы связаны с кубическими членами в выражении для потенциальной энергии (5.8.1). Члены со степенями выше третьей определяют четырёх фононные и более сложные процессы рассеяния.

Переход от картины невзаимодействующих звуковых волн («гармонических» фононов) в гармоническом приближении к картине взаимодействующих звуковых волн в реальном кристалле требует введения

«ангармонических» фононов. Взаимодействие фононов, в результате которого возникает передача энергии от одного фонона к другому, возможно только в том случае, когда частотный спектр каждого фонона становится непрерывным в некоторой области частот вблизи основной частоты w_i. В гармоническом приближении частотный спектр фонона описывается δ-функцией аргумента w - w_i. Возможность передачи энергии от одного фонона другому определяется перекрытием между собой областей размытия спектра различных фононов, как это схематически показано на рис. 5.8.2. Чем больше степень ангармоничности колебаний, тем сильнее перекрываются эти области, тем эффективнее происходит процесс взаимодействия между фононами и тем быстрее устанавливается тепловое равновесие в твёрдом теле. При этом надо иметь в виду, что в действительности возможность рассеяния фононов друг на друге определяется не только степенью перекрытия их спектров, но и правилами отбора, которые существенно ограничивают взаимодействие в системе фононов.

Поскольку степень ангармонизма колебаний атомов в решётке мала, особенно в области низких температур, где и применима фононная модель, удобно сохранить представление о практически идеальном газе фононов, приписывая каждому фонону некоторое эффективное сечение рассеяния. Таким образом, если невзаимодействующие гармонические фононы представляют собой идеальный газ квазичастиц бесконечно малых размеров, то ангармонические фононы можно рассматривать как слабо-неидеальный газ квазичастиц конечных размеров.

Коэффициент 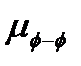фонон-фононного рассеяния для такой модели по аналогии с коэффициентом 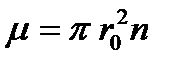рассеяния частиц с радиусом r₀ в идеальном газе с концентрацией n имеет вид

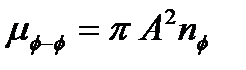(5.8.3)

где 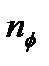- плотность фононов, 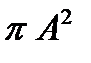- эффективное рассеяние фононов, определяемое коэффициентом ангармонизма. Длина свободного пробега фононов обратно пропорциональна 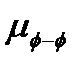· При понижении температуры

возрастает вследствие сильного уменьшения 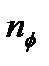(эффект «вымораживания» фононов).

5.8.3. Нормальное рассеяние и процессы переброса. Все процессы взаимодействия фононов можно разделить на две группы: нормальные процессы (N-процессы) рассеяния, в которых сохраняется абсолютное значение волнового вектора фононов

q + q' = q", (5.8.4)

и процессы переброса (U - процессы, от немецкого слова Umklapp - переброс), в которых волновой вектор фонона q" изменяется на вектор обратной решётки g (см. (3.6.4))

q + q' = q" + g. (5.8.5)

Процессы переброса описывают ситуацию, при которой вектор, равный сумме векторов взаимодействующих фононов, выходит за пределы зоны Бриллюэна и попадает, таким образом, в соседнюю эквивалентную по набору волновых векторов зону. При этом выполняется условие (5.8.5), которое означает, что при взаимодействии фононов с волновыми векторами q и q' возникает фонон с волновым вектором q" = q + q' – g. Т.е. изменение волнового вектора q на относительно малую величину q' приводит к появлению фонона с резко отличным по направлению и величине вектором q" (рис. 5.8.3).

U-процессы можно рассматривать как рассеяние, сопровождающееся брэrrовским отражением звуковой волны от решётки. При этом импульс фонона передаётся центру масс решётки. Заметим, что при N-процессах суммарный импульс всех фононов не изменяется, а происходит лишь перераспределение энергии в фононной системе. Принципиальное отличие U-процессов заключается в том, что каждый из них приводит к изменению общего импульса фононной системы. Однако в состоянии равновесия вероятности процессов с изменением импульса на величину g и -g одинаковы, так что в равновесных условиях в результате U - процессов общий импульс фононной системы также не изменяется.

При рассеянии фононов наиболее вероятны трёх фононные процессы. Менее вероятны четырёх фононные процессы, ещё менее вероятны пяти фононные процессы. Возможные трёх- и четырёх фононные процессы показаны на рис. 5.8.4, а и б соответственно. Поляризация фононов при рассеянии может изменяться.

5.8.4. Трёхфононные процессы. Рассмотри м подробнее трёх фононные N-процессы. Начнём с простейшей изотропной модели. Вероятность таких процессов определяется законами сохранения импульса и энергии

q_s + q_s' = q_s". (5.8.6)

Индекс s означает одно из значений L, Т₁, Т₂ (продольные и два типа поперечных фононов).

Зададим некоторое определённое значение вектора q_s = q_L с энергией 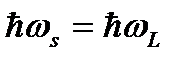и посмотрим, какие требования накладываются на вектор q_s'. соответствующий фонону с энергией 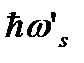и на вектор q_s", соответствующий

фонону с энергией 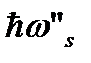. Энергии 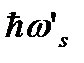соответствует множество векторов q_s', концы которых расположены на трёх поверхностях постоянной частоты 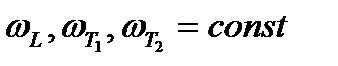(для изотропной модели – на сферах): для одной ветви продольных (L) и двух ветвей поперечных (T₁ и Т₂) фононов. Аналогично энергия 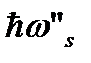определяет три поверхности постоянной частоты, которые задают все возможные значения векторов q”_L, q”_T1 и q”т₂ продольных и поперечных фонoнов с энергией .

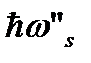Из всего множества векторов q_s' и q_s" закону сохранения импульса удовлетворяют только те векторы, которые образуют с вектором q_s замкнутый треугольник как это показано на рис. 5.8.5, а. Для того, чтобы найти эти векторы, поместим начало системы координат, в которой построены поверхности 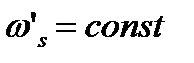, в точку 0', а начало системы координат,

где построены поверхности 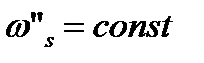в точку О" (рис. 5.8.5, б).

Концы векторов q_s' расположены на одной из поверхностей 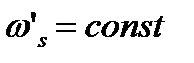, а концы векторов q_s" - на одной из поверхностей 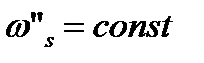. В то же время, в соответствии с законом сохранения импульса они должны сходиться в общей точке Р. Этому требованию удовлетворяют векторы, концы которых образуют геометрическое место точек, расположенных на линиях пересечения поверхностей .

Дата добавления: 2015-10-21