Представление логических функций в виде СДНФ (СКНФ)

Будем использовать логическую функцию “эквивалентность”, записанную в виде х^у. Напомним, что 0⁰= 1; 0¹=0; 1⁰= 0; 1¹= 1.Таким образом, х^у = 1 тогда и только тогда, когда х = у.

Лемма. Любая логическая функция f (x ₁, x ₂, …, x_n) может быть представлена в виде дизъюнкции 2 ^п дизъюнктных слагаемых, причем дизъюнкция берется по всевозможным наборам из Eⁿ. Этот факт будем записывать следующим образом:

(*)

где дизъюнкция проводится по всевозможным наборам (s₁, s₂, …, s _п) из Е^п.

Доказательство леммы.

а) Пусть f (x ₁, x ₂, …, x_n)= 1. Тогда слева в формуле (*) стоит 1. Докажем, что и справа в этом случае стоит 1, для чего достаточно указать одно дизъюнктное слагаемое, равное 1. Но среди всех наборов (s₁, s₂, …, s _п) имеется набор s₁ = х ₁, s₂ = х ₂, …, s _п = х_п. Очевидно, что для этого набора слагаемое 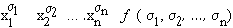равно 1 (так как и .

б) Пусть f (x ₁, x ₂, …, x_n) = 0. Предположим, что справа стоит не ноль, а единица, тогда какое-то слагаемое тоже должно равняться 1, т. е. для некоторого набора

Это означает (по свойствам конъюнкции), что , откуда следует, что х ₁=s₁, х ₂=s₂ , …, х_п =s_n, но в этом случае f (s₁, s₂,..., s_n) f (x _1, x ₂, …, x_n) = 0 и, значит, справа нет слагаемого, равного 1, т. е. в этом случае и справа и слева в формуле (*) стоит 0. Лемма доказана.

Теорема. Если булева функция не равна тождественному нулю, то ее можно представить в виде СДНФ по ее таблице истинности следующим образом: берем только те наборы переменных (х ₁, х _2, …, х_{n )}, для которых f (х ₁, х ₂, …, х_n) =1, и составляем простую конъюнкцию для этого набора так: если х_i = 0, то берем в этой конъюнкции , если х_i = 1, то берем х_{i .} Составляя дизъюнкцию этих простых конъюнкций, придем к СДНФ.

Доказательство. Пусть f (x _1, x ₂, …, x_n) не равна тождественному нулю, тогда в дизъюнкции можно не записывать слагаемые, равные нулю, а из формулы (*) следует следующее представление для данной функции

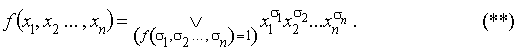
Запись означает, что дизъюнкция берется по всем наборам (s₁, s₂,..., s_n), для которых f (s₁, s₂,..., s_n) = 1. Так как (если s₁=0), из формулы (**) следует утверждение теоремы.

Следствие. Любую логическую (булеву) функцию можно выразить через три логические функции: конъюнкцию, дизъюнкцию и отрицание.

Из предыдущей теоремы видно, что следствие верно для любой функции, не равной тождественному нулю. Однако если f (x ₁, x ₂, …, x_{n ) =}0, то ее также можно выразить через конъюнкцию, дизъюнкцию и отрицание, например, так: f (x ₁, x ₂, …, x_{n ) = x1} ,и, несмотря на то, что последнее выражение не является простой конъюнкцией (и, значит, не является СДНФ), тем не менее тождественный ноль также выражен через нужные три функции.

Набор функций, через которые можно выразить любые другие функции, называется полным набором (более точные формулировки даны в разд. 7). Таким образом, конъюнкция, дизъюнкция и отрицание являются полным набором.

По аналогии с представлением любой функции (не равной тождественному нулю) в виде СДНФ можно функцию (не равную тождественной 1) представить в виде СКНФ: простая дизъюнкция составляется для тех наборов переменных (х ₁, х ₂, …, х_п), для которых f (x ₁, x ₂, …, x_n) = 0, причем если х_i = 1, то в этой дизъюнкции берем _, если же х_i = 0, то берем х_i.

Пример. Составить для импликации и сложения по модулю 2 СДНФ и СКНФ.

х	у	х ® у	х + у

Тогда СДНФ для этих функций:

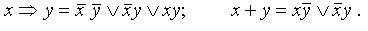
СКНФ для этих функций:

Дата добавления: 2015-10-21