Полиномы Жегалкина

Полиномом (многочленом) Жегалкина от п переменных называется функция

P = a₀ + a₁x₁ +a₂x₂ +...a_nx_n +a_{n +1}x₁x₂ +...+a_{n +C}²_nx_n-1x_n +...+a_2n-1x₁x₂..xn

Всего здесь 2 ^п слагаемых. Напомним, что + сейчас означает сложение по модулю 2, коэффициенты a₀, a₁,..., a₂ⁿ_-1 являются константами (равными нулю или единице).

Теорема. Любая функция п переменных может быть представлена полиномом Жегалкина и это представление единственно.

Доказательство. Любая функция f(x ₁, x ₂, …, x_n) имеет свою таблицу истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределенными коэффициентами. Затем по очереди подставляем всевозможные наборы переменных и находим коэффициенты. Легко видеть, что за каждую подстановку находим только один коэффициент. Так как число наборов равно числу коэффициентов (и равно 2 ^п), отсюда следует утверждение теоремы.

Доказательство этой теоремы показывает, как по таблице истинности построить полином Жегалкина.

Имеется 2-й способ нахождения полинома Жегалкина для функций, заданных в виде ДНФ. Этот способ основан на том, что х +1 = . Если функция задана в виде ДНФ, то сначала убираем дизъюнкцию, используя при этом правило де Моргана, а все отрицания заменяем прибавлением единицы. После этого раскрываем скобки по обычным правилам, при этом учитываем, что четное число одинаковых слагаемых равно нулю (так как х+ х = 0), а нечетное число одинаковых слагаемых равно одному такому слагаемому.

Пример.

(xy + 1)((x + 1)(y + 1) + 1)((y + 1)z + 1) + 1 = (xy + 1)(xy + x + y)(yz + z + 1) + 1 = (x + y)(yz + z + 1) + 1= xyz + yz + xz +yz + x + y + 1 = xyz + xz + x +y + 1.

Последнее выражение и есть полином Жегалкина данной функции.

Функция f (x ₁, x ₂, …, x_n) называется линейной, если ее полином Жегалкина содержит только первые степени слагаемых. Более точно функция называется линейной, если ее можно представить в виде

f(x ₁, x ₂, …, x_n) = a₀ + a₁ x ₁ + a₂ x ₂ +…+ a _n x_n.

Класс линейных функций часто обозначают через L. (Заметим, что число линейных функций п переменных равно 2 ^{п+ 1} ).

Замечание. Если п ³2 то линейная функция в таблице истинности может содержать только четное число единиц. Действительно, если f(x ₁, x ₂, …, x_n) = x ₁ + x ₂ +…+x_{n ,} то легко видеть что такая функция в таблице истинности содержит одинаковое число нулей и единиц а именно 2 ^п / 2 единиц и нулей, т. е. число это четно при п ³2. Столько же нулей и единиц имеет функция 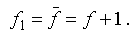.Добавлениежефиктивнойпеременной приводитк увеличению числа единиц (и нулей) в два раза. Разумеется, нелинейная функция может иметь в таблице истинности как четное, так и нечетное число единиц.

Дата добавления: 2015-10-21