Графи з кольоровими ребрами

Існують графи, які відповідають таким ситуація, в яких одні пари елементів множини знаходяться між собою в одному відношенні, інші пари цієї множини – в іншому відношенні, треті – в третьому (але кожна пара – в одному відношенні). Наприклад, серед учасників шахматного турніру на деякий момент можуть бути такі, які уже зіграли партію один з одним, і такі, які ще не зіграли. Для зручності на малюнках графів ребра, що відповідають одному відношенню зафарбовують в один колір, а ребра, що відповідають іншому відношенню – в інший колір і т. д. Такі графи називають графами з кольоровими ребрами. Вони допомагають розв’язати багато задач.

Властивості графів з кольоровими ребрами:

1) Будь-яка вершина повного графа з шістьма або більше вершинами і ребрами двох кольорів, належать не менше ніж трьом ребрам однакового кольору.

2) В довільному повному графі з шістьма чи більше вершинами і ребрами двох кольорів, знайдеться не менше ніж один трикутник з сторонами одного кольору.

3) Якщо в повному графі з 5 вершинами і ребрами двох кольорів не знайдеться трикутника з сторонами одного кольору, то граф можна зобразити у вигляді п’ятикутника з червоними сторонами і синіми діагоналями.

4) В довільному повному графі з 6 чи більше вершинами і ребрами одного з двох кольорів завжди знайдуться два різних трикутники з сторонами одного кольору. Ці трикутники можуть мати спільну вершину чи ребро.

5) В повному графі з 17 чи більше вершинами і ребрами трьох кольорів завжди знайдеться не менше, ніж один трикутник з сторонами одного кольору.

1.5Орієнтовані графи

Ребро графа називаються орієнтованим, якщо одну його вершину вважати початком ребра, а іншу – кінцем.

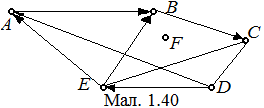
На малюнках орієнтоване ребро позначають стрілкою (мал. 1.40). В тексті орієнтоване ребро з початком A і кінцем B позначають <A;B >. Кажуть, орієнтоване ребро виходить з A і входить в B.

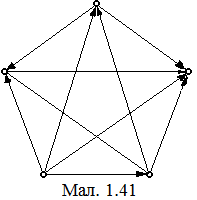Граф, всі ребра якого орієнтовані, називається орієнтованим графом (мал. 1.41).

Одна і та ж вершина орієнтованого графа може служити початком для одних ребер і кінцем для інших. Тому розрізняють два степені вершини: степінь виходу і степінь входу.

Степенем виходу вершини A орієнтованого графа називається число ребер, що виходять в A (степ. вих. A).

Степенем входу вершини A називається число ребер, що входять в A (степ. вх. A).

Наприклад, на мал. 1.40:

степ. вих. D =3; степ. вх. D =0; степ. вих. C =0; степ. вх. C =3, степ. вих. F =0; степ. вх. F =0.

Повним орієнтованим графом називається граф, кожна пара вершин якого з’єднана одним орієнтованим ребром.

Висновки до розділу 1

В цьому розділі ми познайомилися з основними поняттями теорії графів: вершинами, ребрами, степенем вершини, повним графом, доповненням до графа, шляхом у графі. Ми дізналися який граф є повним, який є зв’язним. Це знайомство відбулося через розв’язування конкретних задач прикладного характеру.

Також ми познайомилися з графом “дерево” та “ліс” та розглянули властивості таких графів. За допомогою таких графів розв’язували задачі, перевівши попередньо їх зміст на мову графів. Проте для розв’язування деяких задач цих знань виявилося недостатньо, тому ми познайомилися з графами із кольоровими ребрами та орієнтованими графами, та познайомилися з властивостями таких графів. Використовуючи цей матеріал в другому розділі ми спробуємо розв’язати складні математичні задачі прикладного характеру та розв’язати деякі олімпіадні задачі.

РОЗДІЛ 2

ЗАСТОСУВАННЯ ГРАФІВ

2.1 Графи допомагають розв’язувати задачі

Розглянемо декілька задач, в розв’язуванні яких суттєво допомагають графи з кольоровими ребрами.

Задача. 1 У трьохвимірному просторі 9 точок розміщені так, ніякі три з них не лежать на одній прямій. Кожна точка з’єднана відрізками з чотирма іншими. Доведіть, що завжди знайдеться хоча б один трикутник з вершинами в цих точках.

Розв’язування

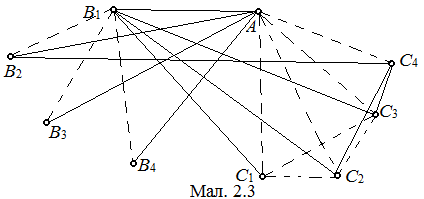
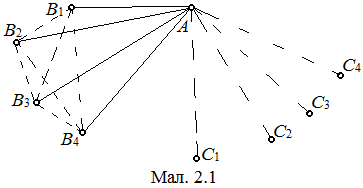
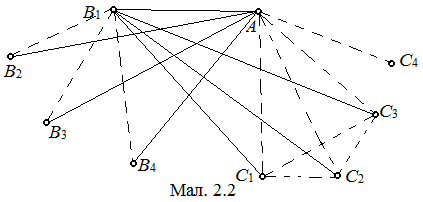Точками простору поставимо у відповідність вершини графа. Проведеному відрізку поставимо у відповідність червоне ребро, не проведеному – синє. Доведемо, що в повному графі з 9 вершинами, кожна з яких належить чотирьом червонимребрам і 4 синім, знайдеться трикутник з червоними сторонами. Припустимо, що такого трикутника не існує. Нехай деяка вершина A з’єднана червоними ребрами з B ₁, B ₂, B _3, B ₄ , синіми з C ₁, C ₂, C ₃, C ₄ (мал 2.1). Кожна із вершин B_i з’єднана трьома червоними ребрами з вершинами C_j. Два червоних ребра з’єднують вершини виду C між собою (оскільки червоних ребер (B_i, C_j) – 12. Нехай B ₁ зв’язана червоними ребрами з C ₁, C ₂, C ₃. Між собою C ₁, C ₂ і C ₃ з’єднані синіми ребрами, інакше утворився б трикутник з червоними сторонами (мал. 2.2). Тоді C ₄ належить двом червоним ребрам виду (C ₄, C_j), наприклад, (C ₄, C ₃) і (C ₄, C ₂). Але ж C ₄ належить ще двом червоним ребрам. Одне з них, наприклад (C ₄, B ₂) (мал. 2.3). Хоч би одне з ребер (B ₂, C ₂) і (B ₂, C ₃) також червоне, тобто хоч би один з трикутників B ₂ C ₃ C ₄ і B ₂ C ₂ C ₄ має червоні сторони.

Задача 2. Доведіть, що в будь-якій групі з дев’яти чоловік, в якій не знайдеться троє попарно знайомих, знайдеться четверо попарно знайомих.

Розв’язування

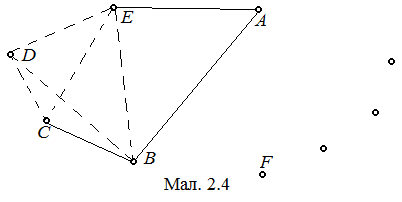Кожній людині з групи поставимо у відповідність вершину графа. Нехай синє ребро означає, що двоє взаємно знайомі, а червоне – не знайомі. По умові немає жодного трикутника з червоними сторонами. Треба довести, що в такому графі існує чотирикутник з синіми сторонами і синіми діагоналями. Нехай в такому графі існує вершина A, яка належить чотирьом, чи більше червоним ребрам (A, B), (A, C), (A, D),(A, E).

Так як червоного трикутника бути не може, то вершини B, C, E, D сполучені попарно синіми ребрами. Отже, BCDE – шуканий чотирикутник.

Тепер розглянемо випадок, коли в графі не існує вершини, яка належить чотирьом і більше червоним ребрам. Нагадаємо, що з кожної вершини не може виходити три червоних ребра. Достатньо розглянути випадок, коли в графі існує вершина, що належить двом або менше червоним ребрам. Тоді ця вершина належить найймовірніше шести ребрам синього кольору. Серед шести вершин – протилежних кінців цих синіх ребер знайдеться трикутник з однаково зафарбованими сторонами. Так як він не може бути червоним, то він є синім.

Задача 3. В місті n жителів. Будь-які двоє з них або дружать, або ворогують, причому серед трьох будь-яких жителів або всі троє дружать, або дружать тільки двоє. Доведіть, що якщо не всі жителі цього міста друзі, то знайдеться житель, у якого ворогів більше, ніж друзів.

Розв’язування

Кожному жителю поставимо у відповідність вершину графа. Нехай синє ребро означає, що двоє дружать, червоне – ворогують. По умові задачі в даному графі можуть бути трикутники або з трьома синіми сторонами, або з однією синьою і двома червоними і є хоча б одне червоне ребро. Треба довести, що знайдеться вершина, червоний степінь якої більше, або дорівнює її синьому степеню. Розглянемо деяке червоне ребро (A, B). Нехай синій степінь вершини A дорівнює k. Припустимо, що k ≥ . Очевидно, що B сполучена червоними ребрами з тими вершинами, з якими A з’єднана синіми ребрами. Тому, якщо червоний степінь вершини B дорівнює l, то:

l=k+ 1> k≥ .

Також,для розв’язування деяких задач використовують орієнтовані графи. Повні орієнтовані графи допоможуть прояснити особливості ситуації, яка зустрічається досить часто, але особливості їх зазвичай залишаються непоміченими. Така задача називається парадокс “голосування з перевагою”.

Задача 4. Чотирьом учням: Іванову, Петрову, Сидорову і Карпову, доручили від імені класу вибрати подарунок іменинниці Каті (Карпов – староста класу, в випадку рівного розподілення голосів, його голос – вирішальний). Після довгих суперечок хлопці зупинились на чотирьох предметах:

1) Ракетка для гри в бадмінтон – Р.Б.

2) Набір для гри в настільний теніс – Н.Т.

3) Волейбольний м’яч – В.М.

4) Морська свинка – М.С.

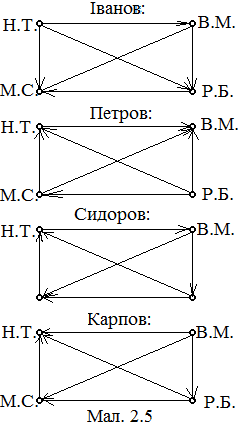
При обговоренні виявилось, що по відношенню до цих предметів у кожного з хлопців своя система переваг. Системи ці представляють собою повні орієнтовані графи з чотирма вершинами (мал. 2.5). Стрілка від однієї вершини то іншої означає, що перша вершина має перевагу над другою. Наприклад, стрілка від В.М. до Р.Б. на мал. 2.5(а) означає, що Іванов при порівнянні волейбольного м’яча і бадмінтону надає перевагу волейбольному м’ячу. По малюнках читаємо, що Іванов найбільше перевагу надає настільному тенісу, Петров – ракетці для бадмінтону, Карпов – волейбольному м’ячу, Сидоров не віддає великої переваги жодному з предметів.

Хлопці домовились про систему вибору подарунка, яка на перший погляд не викликає заперечень. Вирішили вибирати більшістю голосів (кожен голосує відповідно до своїх вподобань) один з двох предметів в такому випадку:

1) Або Б.М., або Р.Б.;

2) Або предмет, що отримає більшість голосів на першому етапі голосування, або Н.Т.;

3) Або предмет, що отримає більшість голосів на другому етапі голосування, або М.С..

Який же подарунок вони повинні вибрати при цій системі голосування?

Слідкуємо по графах на мал. 2.5.

На першому етапі голосування при порівнянні В.М. і Р.Б. більшість голосів (Іванов, Сидоров і Карпов) повинні були отримати В.М.

На другому етапі при порівнянні В.М. і Н.Т. більшістю голосів (Іванов, Петров і Сидоров) повинні були вибрати Н.Т.

На третьому етапі при порівнянні Н.Т. і М.С. більшістю голосів (Петров, Сидоров, Карпов) повинні були вибрати М.С.

Раптом виявляється, що четверо вибирають подарунок – морську свинку, хоча ні один з хлопців не надавав переваги цьому подарунку.

В структурі такого голосування все вирішив порядок, в якому порівнювались пари предметів. Чим пізніше предмет бере участь у виборі, тим вищий у нього шанс бути вибраним.

Якщо б, наприклад, Іванов вник в особливості системи голосування з перевагою і йому дуже хотілося подарувати Каті набір для гри в настільний теніс, то він запропонував би товаришам замінити порядок порівняння предметів так, щоб настільний теніс розглядався тільки в останній парі. Тоді, які б пари не порівнювались на першому і другому етапах голосування, був би вибраний набір для настільного тенісу.

2.2 Олімпіадні задачі

При розв’язуванні багатьох олімпіадних задач іноді використовують графи – дуже популярного об’єкта дискретної математики.

Задача 1. Є 30 осіб, серед яких деякі знайомі між собою. Доведіть, що кількість осіб, які мають непарну кількість знайомих, парна.

Розв’язування

Розглянемо граф, який відповідає умові задачі і біля кожної його вершини напишемо по числу – кількість ребер, які з неї виходять (степінь вершини). Тоді сума всіх цих чисел – число парне (воно в 2 рази більше за кількість ребер). Звідси випливає, що непарних доданків у цій сумі мусить бути парна кількість, що і треба було довести.

Задача 2. У графа 100 вершин, причому степінь будь-якої з них не менший за 50. Доведіть, що граф зв’язний.

Розв’язування

Припустімо, що це не так, тоді він складатиметься з граф (підграфи), не зв’язних між собою. Нехай k – кількість вершин одного з них, причому k – найменше. Тоді k≤ 50. Але степінь кожної вершини такого графа не більше 49. Отримали протиріччя. Отже припущення неправильне.

Задача 3. В орієнтованому графі 101 вершина. У кожної вершини кількість ребер, які з неї виходять, дорівнює кількості ребер, що в неї входять, причому ця кількість дорівнює 40. Доведіть, що з будь-якої вершини можна попасти у будь-яку іншу, пройшовши не більше, як по трьох ребрах.

Розв’язування

Нехай a і b – дві вершини графа, A – множина, яка складається з 40 вершин, з яких йдуть ребра у вершину b, C – множина вершин, які залишились.

Припустимо, що з a не можна попасти в вершину b по трьох ребрах. Тоді всі ребра, які виходять з A, йдуть в A чи в С. Таких ребер за умовою всього 40×40=1600. Але ребер, які знаходяться в A не більше, ніж 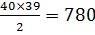, а ребер, які виходять з A в С не більше, ніж 40×19=760. Але 780+760=1540<1600. Отримали протиріччя. Отже припущення невірне.

Задача 4. У графа 20 вершин, степінь яких не менший 10. Доведіть, що в ньому є шлях, по якому можна обійти всі вершини, побувавши в кожній по одному разу.

Розв’язування

Виберемо найдовший шлях, в якому вершини не повторяються. Припустимо, що він містить не всі вершини. Тоді, в нього є дві вершини, одна з яких з’єднана з кінцем шляху, а друга з вершиною, яка не належить шляху. Маючи такі вершини, неважко збільшити шлях.

Висновки до розділу 2

В цьому розділі ми розглянули питання застосування графів при розв’язуванні різних задач. Зокрема для розв’язування задачі 1, яка є геометричною, ми застосували теорію графів з кольоровими ребрами, за допомогою якої ця задача розв’язується просто. Дві інші задачі прикладного характеру, які можна віднести до теми “соціологія” розв’язані також за допомогою графів з кольоровими ребрами.

Дуже часто в математиці зустрічається задача, яку називають парадокс “голосування з перевагою”. Цю задачу ми розв’язали за допомогою орієнтованих графів.

Олімпіадні задачі вважаються одними з найскладніших. Ми намагалися показати, як розв’язуються такі задачі за допомогою теорії графів.

Дата добавления: 2015-10-13