Зображення графа

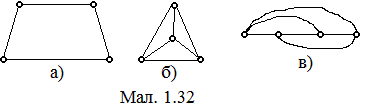Один і той же граф може виглядати по різному. Наприклад, на трьох малюнках 1.32 (а), (б), (в), мало схожих один на одного, зображено один і той же граф (повний з 4 вершинами).

Щоб переконатися в тому, що два малюнки зображають один і той же граф, необхідно перевірити:

1. Чи однакове число вершин на обох малюнках?

2. Чи однакове число ребер?

3. Чи однакове число вершин має степінь k?

Але виконання трьох перерахованих умов ще не достатньо для того, щоб два малюнки зображали один і той же граф. Дійсно, на малюнках 1.33(а) та 1.33(б) зображено графи, що мають по 7 вершин, по 10 ребер, причому по одній вершині з степенем 4, по чотири вершини з степенем 3, по дві вершини з степенем 2.

Але ж, ці малюнки зображають різні графи, так якщо на мал. 1.33(б) вершини з степенем 2 (B₆ і B₇) ребрами не з’єднані.

Сформулюємо необхідну і достатню умову відповідності двох малюнків одному і тому ж графу. Малюнки зображають один і той же граф тоді і тільки тоді, коли між вершинами на першому і другому малюнках існує така взаємно однозначна відповідність, при якій:

· Дві вершини графа першому малюнку з’єднані ребром, якщо з’єднана ребром відповідна пара вершин графа на другому малюнку.

Доведемо, що на мал. 1.34(а) і 1.34(б) зображено один і той же граф.

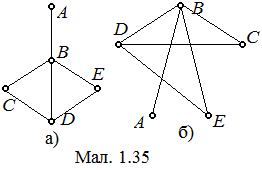На цих малюнках зображені графи з однаковим числом вершин, однаковим числом ребер; на кожному з них – по одній вершині з степенем 3, по дві вершини з степенем 1. Вершини, які поставимо у взаємно однозначну відповідність, позначимо однаковими буквами (мал. 1.35).

При такій відповідності вершини позначені однаково, мають однакові степені, і якщо будь-які дві вершини на мал. 1.35(б) з’єднані ребром. Це дозволяє робити висновок, що на мал. 1.35(а) і 1.35(б) зображено один і той же граф.

Щоб вияснити, чи відповідають два малюнки одному і тому ж графу, деколи досить важко. Особливо важко тоді, коли малюнок має багато вершин і багато ребер.

В першу чергу треба порівняти число вершин, число ребер, число вершин з однаковими степенями; якщо вони співпадають на обох малюнках, то встановлюють взаємно-однозначну відповідність вершин. Після цього перевіряють виконання необхідної і достатньої умови відповідності двох малюнків одному і тому ж графу. Звичайно, якщо ці дві умови не виконуються, то ще не можна робити висновок, що на малюнках зображені різні графи, так як можливо була невірно встановлено взаємно-однозначна відповідність між вершинами.

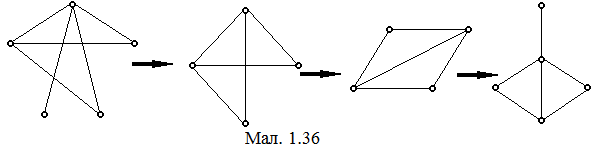
В попередньому прикладі встановити відповідність двох малюнків одному і тому ж графе ще легше було б геометрично (мал. 1.36). Але описаний спосіб шляхом встановлення взаємно-однозначної відповідності вершин є більш ефективним, якщо у графі багато вершин і ребер.

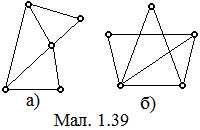
Приклади зображення одного і того ж графа на мал. 1.37 (а) і (б), на мал. 1.38 (а) і (б), на мал. 1.39 (а) і (б).

Дата добавления: 2015-10-13