Повний граф. Доповнення графа

Граф називається повним, якщо дві різні вершини його з’єднані одним і тільки одним ребром(мал. 1.11)

В повному графі кожна його вершина належить одному і тому ж числу ребер. Щоб задати повний граф, достатньо знати число його вершин.

Граф, що не є повним, можна перетворити в повний, з тими ж вершинами, добавивши ребра, яких не вистачає.

Наприклад граф Г на мал. 1.14 неповний. Провівши ребра, яких не вистачає, отримаємо повний граф з п’ятьма вершинами. Вершини графа Г і ребра, які провели, також утворюють граф. Він зображений на мал. 1.16. Такий граф називають доповненням графа Г і позначають його .

Вершини в графі можуть відрізнятися одна від одної тим, скільком ребрам вони належать.

Степінь вершини

Степенем вершини називають число ребер графа, яким належать ця вершина.

Степінь вершини позначають: степ. A =1, степ. B=2.

У графа на мал. 1.17(а): степ A =1, степ. B =2. У графа на мал. 1.17(в) степені всіх вершин дорівнюють нулю.

Вершина називається парною, якщо її степінь – число парне; вершина називається непарною, якщо її степінь – число непарне.

Маючи навіть загальні уявлення про граф, інколи можна судити про степінь його вершин. Так степінь кожної вершини повного графа на одиницю менший за число його вершин. При цьому деякі закономірності пов’язані з степенями вершин, є не тільки в повних графів.

Наприклад:

Задача 1. Учасники міжнародної математичної олімпіади, познайомившись, обмінялись конвертами з адресами. Доведіть що:

а) всього було передано парне число конвертів;

б) число учасників, що обмінялися конвертами непарне число разів, парне.

Розв’язування

Нехай учасники олімпіади A ₁, A ₂, A ₃,..., A_n – вершини графа, а ребра, сполучають на мал. 1.18 пари вершин, зображають учасників, що обмінялись конвертами.

а) Степінь кожної вершини A_k показує число конвертів, які передав учасник A_k своїм знайомим. Загальне число переданих конвертів N дорівнює сумі степенів вершин графа.

N= степ A ₁+ степ A ₂+…+ степ A_n-1+ степ A_n, але N=2p, де p – число ребер графа, тобто N – парне. Отже, було передано парне число конвертів.

б) В сумі N= степ A ₁+ степ A ₂+…+ степ A_n-1+ степ A_n сума парних доданків повинна бути парною, а це може бути тільки в тому випадку, якщо число непарних доданків парне. А це значить, що число учасників, що обмінялися конвертами непарне число разів, парне.

Вході розв’язування задачі 1 ми довели дві теореми.

Теорема 1

В графі Г сума ступенів всіх його вершин – число парне, і дорівнює подвоєному числу ребер графа.

, де p – число ребер графа Г, n – число його вершин.

Теорема 2

Число непарних вершин довільного графа повне.

Можна виявити і інші цікаві властивості графів.

Розглянемо спочатку графи з 5-ма ребрами. Степінь кожної вершини такого графа приймає одне з значень 4, 3, 2, 1, 0. Для цього розв’яжемо такі задачі.

Задача 3. Дев’ять шахматистів проводять турнір в один круг (кожен з учасників повинен зіграти з кожним із решти по одному разу). Доведіть, що в будь-який момент знайдуться двоє, що зіграли однакове число партій.

Розв’язування

Переведемо умову задачі в на мову графів. Кожному з шахматистів поставимо у відповідність вершину графа, сполучимо ребрами попарно вершини, що відповідають шахматистам, які уже зіграли між собою партію. Отримаємо граф з дев’ятьма вершинами. Степені його вершин дорівнюють числу партій, які зіграли певні гравці. Покажемо, що в усякому графі з дев’ятьма вершинами завжди знайдеться хоча б дві вершини з однаковими степенями.

Кожна вершина графа з дев’ятьма вершинами може мати степінь, що дорівнює 0, 1, 2, 3, 4, 5, 6, 7, 8. Припустимо, що існує граф Г, всі вершини якого мають різні степені, тобто кожне із чисел послідовності 0, 1, 2, 3, 4, 5, 6, 7, 8 є степенем одної і тільки одної його вершини. Але ж такого бути не може. Дійсно, якщо в графі є вершина A з степенем 0, то в ньому немає вершини B з степенем 8, так як ця вершина B повинна бути сполучена з рештою вершин графа, в тому числі і з вершиною A. Тобто в графі з дев’ятьма вершинами не можуть бути одночасно варіанти з степенями 0 і 8. Отже, знайдуться хоча б дві вершини з однаковими степенями.

Розв’язування цієї задачі дослівно повторюється в ході доведення наступної теореми (тільки число 9 замінимо довільним натуральним числом n≥ 2).

Теорема 3

В будь-якому графі з n вершинами, де n≥ 2, завжди знайдеться не менше двох вершин з однаковими степенями.

Розв’яжемо ще одну задачу, пов’язану степенями вершин.

Задача 4. Дев’ять чоловік проводять шахматний турнір в один круг. На деякий момент виявляють, що двоє зіграли однакове число партій. Довести, що тоді ж один з учасників ще не зіграв жодної партії, або один з учасників зіграв всі партії.

Розв’язування

Умову задачі переведемо на мову графів. Нехай вершини графа – шахматисти, а кожне ребро означає, що відповідні гравці уже зіграли між собою партію. Із умови відомо, що дві вершини мають однокові степені. Треба довести, що в такому графі завжди знайдеться або тільки одна ізольована вершина, або тільки одна вершина з степенем 8.

В загальному випадку у графа з дев’ятьма вершинами степінь кожної вершини може набувати тільки одне з дев’яти значень: 0, 1, 2, 3, 4, 5, 6, 7, 8. Але у такого графа степені вершин можуть набувати тільки 8 різних значень, отже рівно дві вершини мають однакові степені. Отже обов’язково або 0, або 8 буде значенням степеня однієї з вершин.

Доведемо, що в графах з дев’ятьма вершинами, дві з яких мають однакові степені, не може бути двох вершин з степенем 0, або двох вершин з степенем 8.

Припустимо, що все ж таки знайдеться граф з дев’ятьма вершинами, в якому рівно дві вершини ізольовані, а всі решта мають різні степені. Тоді, якщо не розглядати ці дві ізольовані вершини, залишиться граф з сімома вершинами, степені яких всі різні. Але ж такого графа не існує (див. теорему 3). Значить, це припущення невірне.

Тепер припустимо, що існує граф з дев’ятьма вершинами в якому рівно дві вершини мають степінь 8 а всі решта – різні степені. Тоді доповненням даного графа буде граф, дві вершини якого мають степінь 0, а решта попарно різні степені. Але і цього також не може бути, згідно теореми 3.

Значить, у графа з дев’ятьма вершинами, з яких точно дві мають однакові степені, завжди знайдеться або одна ізольована, або вершина з степенем 8.

Повернемося до задачі. Серед дев’яти шахматистів, яких ми розглядаємо, або тільки один не зіграв жодної партії, або тільки один зіграв всі партії. При розв’язуванні цієї задачі число 9 можна було замінити любим іншим числом n >2.

За допомогою розв’язування цієї задачі легко можна було довести теорему 4.

Теорема 4

Якщо в графі з n вершинами (n >2) точно дві вершини мають однакові степені, то в цьому графі завжди знайдеться одна вершина з степенем 0, або одна вершина з степенем (n -1).

Шлях у графі. Цикл

Як пройти по ребрах на мал. 1.19 з A ₁ в A ₅?

Ось три послідовності ребер, рухаючись по яких можна попасти з A ₁ в A ₅:

1. (A ₁, A ₄); (A ₄, A ₅).

2. (A ₁, A ₂); (A ₂, A ₄), (A ₄, A ₅).

3. (A ₁, A ₄); (A ₄, A ₂); (A ₂, A ₁); (A ₁, A ₄); (A ₄, A ₅).

В одних – ребра повторюються, в інших не повторюються. Можна вказати маршрут від A ₁ до A ₅, який включає всі вершини графа. Наприклад: (A ₁, A ₂); (A ₂, A ₄); (A ₄, A ₃); (A ₃, A ₁); (A ₁, A ₄); (A ₄, A ₅). Але не будь-яку послідовність ребер, що ведуть з A ₁ в A ₅ називають шляхом з A ₁ в A ₅.

Шляхом з A ₁ в A_n в графі називають таку послідовність ребер, які ведуть з A ₁ в A_n, в якій кожні два сусідні ребра мають спільну вершину, і ніяке з ребер не повторюється більше ніж один раз.

Вершина A ₁ – початок шляху, вершина A_n – кінець. Із означення видно, що послідовність (3) не є шляхом в графі. Також, згідно означення, вершини шляху можуть повторюватись, тобто шлях може бути з само перетинами. Шлях з A ₁ в A_n називається простим, якщо він не проходить через жодну з вершин більше, ніж один раз.

Циклом називають шлях, в якому співпадають його початкова і кінцева вершини.

Простим циклом у графі називається цикл, що не проходить ні через жодну вершину більше, ніж один раз.

Довжиною шляху називається число ребер цього шляху.

Довжиною циклу називають число ребер в цьому циклі.

Від вершини A ₁ до вершини A ₆ графу на мал. 1.20 можна пройти чотирма шляхами. Один з них має довжину 1 (A ₁, A ₆), другий – довжину 2 ((A ₁, A ₂); (A ₂, A ₆)), і два мають довжину 6.

Теорема 5

Якщо у графа всі прості цикли парної довжини, то граф не має жодного циклу непарної довжини

Доведення

Для графа, що є простим циклом, твердження теореми очевидне.

Припустимо, що у графа всі прості цикли якого парної довжини, все ж знайдеться цикл непарної довжини. В будь якому непростому циклі існує вершина, через яку шлях проходить більше ніж один раз. В такій вершині цикл розіб’ється на два, причому один з них буде мати парну довжину, а другий – непарну. Будемо продовжувати ділити непарний цикл до того часу, поки не отримаємо прості цикли. Хоча б один з них повинен мати обов’язково непарну довжину. Існування такого простого циклу суперечить умові, отже припущення неправильне.

Поняття шляху у графі привело до поняття зв’язності графа.

Зв’язність графа

Задача 5. Чи може так статися, що в одній компанії з шести чоловік, кожен знайомий з двома і тільки двома іншими?

Розв’язування

Учасника цієї компанії зобразимо вершиною графа, а відношення знайомства між двома учасниками – ребрами. Зобразимо графи, що можуть відповідати такій компанії (мал. 1.21 і мал. 1.22).

Ситуація, що розглядається задачі може можлива. Але випадок, зображений на мал. 1.22, відповідає не одній, а двом компаніям, учасники першої не знайомі з учасниками другої.

Про граф, що зображений на мал. 1.21 кажуть, що він зв’язний, так як із кожної його вершини по ребрах можна попасти в будь-яку іншу вершину.

Отже робимо висновок, що в цьому випадку через своїх знайомих кожен може познайомитися з усіма останніми.

В другому випадку (мал. 1.22) отримали два простих цикли, не з’єднаних між собою в вершинах. Такий граф називається незв’язним.

Дві вершини A і B графа називаються зв’язними, якщо в графі існує шлях з кінцями A і B.

Дві вершини графа називаються незв’язними, якщо в графі не існує жодного шляху, що з’єднує їх.

Наприклад: в графі (мал. 1.23) вершини A і B зв’язні, а вершини A і N – незв’язні.

Граф називається зв’язним, якщо кожні дві його вершини зв’язні.

Граф називається незв’язним, якщо хоча б дві його вершини його незв’язні.

На мал. 1.20 та 1.21 зв’язні графи, а на мал. 1.22та 1.23 – незв’язні графи.

Для зв’язних графів справедливі такі теореми:

Теорема 6 (пряма)

Якщо Г – зв’язний граф і степінь кожної його вершини дорівнює 2, тоді Г – простий цикл.

Теорема 7 (обернена)

Якщо граф Г – простий цикл, тоді кожна його вершина має степінь 2.

Операція видалення ребра. Міст

При видаленні ребра (A, B) із графа Г отримаємо граф з тими ж вершинами, що і граф Г, і всіма ребрами крім ребра(A, B).

Прикладом видалення ребра (A, B) із графа показано на мал. 1.24.

При видаленні ребра із зв’язного графа новий граф може бути як зв’язний так і незв’язний.

Ребро (A, B) називається мостом графа Г, якщо в графі, який отримали після видалення ребра (A, B) з графа Г, вершини A і B стають незв’язними.

На мал. 1.24 міст (A, B) зображено штриховою лінією.

Існує декілька ознак мостів. Розглянемо деякі з них.

1) Ребро (A, B) є мостом тоді і тільки тоді, якщо (A, B) – єдиний шлях що з’єднує вершини A і B (мал. 1.25)

2) Ребро (A, B) є мостом тоді і тільки тоді, якщо знайдеться дві вершини C ₁ і C ₂ такі, що кожен шлях, що з’єднує їх містить A і B (мал. 1.26).

3) Ребро (A, B) є мостом тоді і тільки тоді, якщо воно не належить ні одному з циклів (мал. 1.27).

1.3Дерева. Ліс

Нагадаємо, що з терміном “дерево” ми зустрічались при розв’язуванні задач.

Деревом називається довільний зв’язний граф, що не має циклів (мал. 1.28). Зручно вважати (зручність цю видно при доведенні теореми 8), що граф, який складається з однієї ізольованої вершини, також є деревом.

Для кожної пари вершин дерева існує єдиний шлях, що їх з’єднує. Вершина дерева, степінь, якої дорівнює одиниці, називається висячою вершиною (на мал. 1.28 висячі вершини виділені зафарбованими кружечками).

Лісом називається незв’язний граф, що складається з об’єднання дерев (мал. 1.29, мал. 1.30).

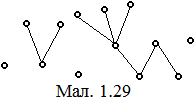
Нагадаємо, що термін “ліс” зустрічався при розв’язуванні задачі.

Будь-яке ребро в дереві (і в лісі) є мостом (ознака 3). Якщо побудувати будь-яке дерево з п’ятьма вершинами і підрахувати число ребер в такому графі, то виявляється, що в будь-якому дереві з п’ятьма вершинами завжди буде чотири ребра.

Теорема 8

Дерево з n вершинами має (n -1) ребро.

Для того, щоб з одного дерева Г, що не є ізольованою вершиною, отримати два дерева з тими ж вершинами, необхідно видалити з Г одне ребро. Для того, щоб отримати три дерева необхідно видалити із Г будь-яких два ребра. Найбільшу кількість із дерева Г з n вершинами, можна отримати з n дерев, кожне з яких є ізольованою вершиною. Для цього необхідно видалити (n -1) ребро з дерева Г. Отже, дійсно, в дереві з n вершинами є (n -1) ребро.

Кубок по настільному тенісу розігрується по олімпійській системі. Зустрічі проводяться без нічиїх. До наступного туру допускається тільки команда, що виграла попередній тур. Ті, що програли, вибувають з гри. Для того, щоб завоювати кубок, команда повинна перемогти у всіх турах.

На участь в розігруванні кубка 16 команд подали свої заявки. Схема проведення ігор зображується графами на мал. 1.31.

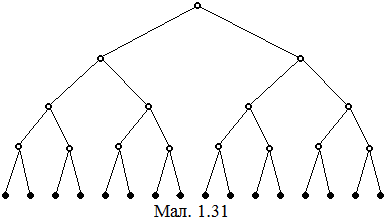
Вершини нижнього “ярусу” дерева (зафарбовані), інтерпретуємо як команди, що беруть участь у розігруванні кубка, вершини другого знизу ярусу – як команди переможниці в 1/16 фіналу, вершини третього знизу ярусу – переможці в 1/8 фіналу і т. д.

Яку інформацію можна отримати за допомогою цього дерева. Безпосередньо з нього можна прочитати:

1) Число всіх учасників розігрування кубка (число зафарбованих вершин).

2) Число етапів проведення розігрування (число “ярусів” з вершин в деревах, не рахуючи нижнього).

3) Число команд, які беруть участь в 1/8 фіналу, в 1/4 фіналу, в 1/2 фіналу (число вершин відповідно в четвертому зверху ярусі, в третьому зверху ярусі, в другому зверху ярусі).

4) Число матчів, які прийдеться зіграти командам для виявлення володаря кубка (число не зафарбованих вершин в графі. До речі, це число легко виявити і без дерева (в кожному матчі вибуває одна команда. Для того, щоб визначити команду-переможницю, решта повинні вибути з змагання. Тому число матчів дорівнює числу команд буз однієї, а саме 15).

Дата добавления: 2015-10-13