Перше знайомство з графами

Ткач Павло Миколайович

Учень 11 класу

Довговільської загальноосвітньої

школи I-III ступенів

Науковий керівник:

Печончик Галина Іванівна

вчитель математики

Довговільської загальноосвітньої

школи I-III ступенів

Довговоля – 2012

ЗМІСТ

ВСТУП 3 РОЗДІЛ 1. Перше знайомство з графами 4

1.1 Задачі, що приводять до графів 4

1.2 Деякі основні поняття теорії графів 8

1.3 Дерева. Ліс 16

1.4 Зображення графа 18

1.5Графи з кольоровими ребрами 20

1.6Орієнтовані графи 21

ВИСНОВКИ ДО РОЗДІЛУ 1 22

РОЗДІЛ 2. Застосування графів

2.1 Графи допомагають розв’язувати задачі 24

2.2Олімпіадні задачі 27

ВИСНОВКИ ДО РОЗДІЛУ 2 29

ВИСНОВКИ 30

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 31

ВСТУП

Інколи для того, щоб розв’язувати різні задачі на смикалку, логічні, олімпіадного типу чи головоломки, то потрібно було складати таблиці, зображати об’єкти точками, та з’єднувати їх відрізками чи стрілками, бачити закономірності у виконаних малюнках, виконувати над точками і відрізками операції, не схожі на арифметичні, алгебраїчні чи на перетворення в геометрії, тобто потрібно було побудувати математичний апарат спеціально для розв’язання задачі. А це означає, що ви заново відкривали для себе початки теорії графів.

Історично склалося так, що теорія графів народилася під час розв’язування головоломок більш як 200 років тому. Дуже довго вона знаходилась осторонь від головних напрямків дослідження вчених, була в царстві математики на правах Попелюшки, таланти якої розкрились в повній мірі тільки тоді, коли вона опинилась в центрі загальної уваги.

Поштовх до свого розвитку теорія графів отримала на рубежі 19 і 20 століть, коли різко виросло число робіт в області топології і комбінаторики. Як окрема математична дисципліна теорія графів була вперше представлена в роботі угорського математика Кеніга в 30-ті роки XX століття.

Останнім часом графи і пов’язані з ними методи досліджень дуже актуальні та органічно пронизують на різних рівнях майже всю сучасну математику. Графи ефективно використовуються в теорії планування і управління, теорії розкладів, соціології, математичній лінгвістиці, економіці, біології, медицині. Широке застосування знаходять графи в таких областях прикладної математики, як програмування, теорія кінцевих автоматів, електроніка, в розв’язуванні задач з теорії ймовірностей і комбінаторних задач. Теорія графів швидко розвивається і знаходить все нові області застосування.

Метою нашої роботи є знайомство з одним із основних об’єктів дискретної математики – теорією графів, для того, щоб навчитись переводити умову розв’язуваної задачі на мову графів.

Це дасть змогу розв’язувати задачі геометричного змісту, соціологічного, комбінаторного і т.д.

РОЗДІЛ 1

ПЕРШЕ ЗНАЙОМСТВО З ГРАФАМИ

1.1 Задачі, що приводять до графів

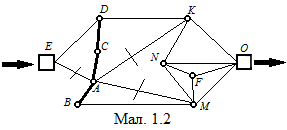
Задача 1. Як ви пам’ятаєте, мисливець за мертвими душами Павло Іванович Чичиков побував у відомих вам поміщиків по одному разу у кожного. Він відвідував їх у такому порядку: Манілова, Коробочку, Ноздрьова, Собакевича, Плюшкіна, Тентетникова, генерала Бетрищева, Пєтуха, Констанжогло, полковника Кошкарьова. Знайдена схема на якій Чичиков зобразив взаємне розміщення помість і польових доріг, що їх з’єднують. Знайдіть, яке помістя кому належить якщо ні по одній з доріг Чичиков не проїжджав більш як один раз.

Розв’язування

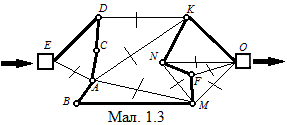
Із схеми видно, що подорож Чичиков почав із помістя E, а закінчив помістям O. В помістя B і C ведуть тільки дві дороги, тому по цих дорогах Чичиков повинен був проїхати. Помітимо їх жирною лінією на мал. 1.2. Визначені ланки маршруту, що проходять через A: AC і AB. По дорогах AE, AK і AM Чичиков не їздив. Перекреслимо їх на малюнку 1.2. Відмітимо жирною лінією ED і перекреслимо DK. Перекреслимо FO; відмітимо жирною лінією FN, NK і KO (мал. 1.3). Знайдем єдино можливий при даній умові маршрут.

Перший підсумок: задача розв’язана в ході перетворення картинки. З малюнка 1.3 читаємо відповідь: помістя E належить Манілову, D – Коробочці, D – Ноздрьову, А – Собакевичу, B – Плюшкіну, M – Тентетникова, F – Бетришеву, N – Пєтуху, K – Констанжогло, O – Кошкарьову.

Задача 2. Листок паперу Плюшкін розрізує на три частини. Деякі з отриманих листків він також розрізує на три частини. Декілька нових листків він знову розрізує на три частини і т.д. Скільки Плющкін отримає листочків паперу, якщо він розрізає k листків.

Розв’язування

Листки паперу позначимо на малюнку кружечками. Кружечки, що відповідають листкам, які розрізали, зафарбовуємо повністю, решту кружечків залишаємо не зафарбованими. Малюнок 1.4 допомагає побачити, що при розрізанні одного листка на три частини число листків збільшується на два
(з’являються три нових замісь одного). Якщо було розрізано k листків, то утворилось 1+2k листків (мал. 1.5).

На малюнку 1.5 показано 5 розрізань. Скільки листків отримали в цьому випадку.

Схеми на малюнках 1.4 і 1.5 дуже нагадують гілку дерева з листочками. Математики звернули увагу на таку схожість і назвали такі схеми “деревами”.

Задача 3. Скільки різних обідів П. І. Чичиков міг нарахувати із страв, виставлених на столі П. П. Пєтухова, якщо б на кожен обід вибирати тільки одну першу, одну другу, одну третю? На столі у П. П. Пєтухова на цей раз були виставлені з холодних страв холодець, свіжа ікра та риба; на перше – уха, борщ з грибами; на друге – смажена осетрина, смажене порося; на третє – кавуни та груші.

Розв’язування

Кожну страву позначимо кружечком, а відповідність страв для кожного обіду – відрізками, що сполучають кружечки, кожен кружечок позначимо першою буквою назви страви. Отримаємо схему зображену на малюнку 1.6. Схема допомагає порахувати число варіантів. Вона ж допоможе дізнатися, скільки різних обідів можна скласти з ікрою, наприклад; скільки різних обідів з кавуном. Отримана схема трохи складніша ніж на малюнку 1.5. Вона складається із трьох дерев. Таку схему називають ”лісом“.

Задача 4. Стверджують, що в одній компанії із п’яти чоловік кожен знайомий з двома і тільки з двома іншими. Чи можлива така компанія?

Розв’язування

Кожного і з цієї компанії позначимо на малюнку кружечком. Якщо двоє знайомі, то сполучимо відповідні кружечки відрізком. Виявляється, що такі ситуації не тільки можливі, але й їх усіх можна описати аналогічними схемами (мал.. 1.7). З цієї компанії не можна виділити ні “чотирикутник”, ні “трикутник”, оскільки тоді з тих, що залишаться, не можна скласти компанію, що задовольняє умові, тобто знайомства єдина. Всяку схему, що нагадує многокутник, називають циклом. (Древні греки “цикл” називали “колесом”, дійсно на мал.1.8 зображено коло, що нагадує колесо, і може замінити в цій ситуації многокутник).

Що ж спільного у схем, які допомогли нам розв’язати ці задачі? Всі вони складаються із точок(кружечків) і відрізків, що сполучають пари точок. Розгляд таких схем і приводить до поняття графа.

Граф – це не порожня множина точок і множина відрізків, обидва кінці

яких належать даній множині точок.

Надалі граф будемо позначати буквою Г. При зображені графів на малюнках чи схемах відрізки можуть бути прямолінійними чи криволінійними; довжини відрізків і розміщення точок довільні.

Всі три фігури на мал.1.9 позначають один і той же граф.

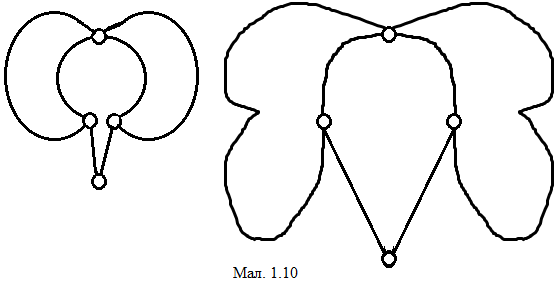
З позиції теорії графів немає відмінності між “мишкою” і “слоном” на мал.1.10.

Точки (кружечки) називаються вершинами, відрізки – ребрами графа. Вершини графа на малюнку виділяють кружечками чи квадратиками хоча б тому, що не завжди точки перетину ребер приймають за вершини графа. Наприклад, по умові на мал..1.11 точка перетину “діагоналей чотирикутника” не є вершиною графа.

Наприклад:

1) На мал. 1.11 зображено граф з 4 вершинами і 6 ребрами.

2) На мал. 1.12 зображено граф з 5 вершинами і 2 ребрами.

3) На мал. 1.13 зображено граф з 3 вершинами і без жодного ребра. Вершини, що не належать жодному з ребер називають ізольованими.

Граф, зображений на мал. 1.12, має одну ізольовану вершину, а в графі на мал. 1.13 всі три вершини ізольовані.

Позначати графи будемо великими літерами латинського алфавіту (A, B, C, … X, Y, …), Ребра графа будемо позначати парою вершин, наприклад (AB), (1,5) і т. д., або малими буквами латинського алфавіту(a, b, c, …, x, y, …).

Деколи ми будемо зображати граф, не позначаючи буквами його вершини і ребра.

Прикладами графів може служити схема метрополітену, схема автомобільних доріг чи залізниці, структурні формули молекул, плани виставок і т.д., тобто схеми і плани без масштабу, які показують лиш зв’язки між об’єктами.

1.2 Деякі основні поняття теорії графів

Дата добавления: 2015-10-13