Теория графов

Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В дальнейшем оказалось, что понятие графа можно применять не только при исследовании геометрических конфигураций. Особенно часто определяют графы при анализе функционирование неких систем.

1. Графы, их вершины, рёбра и дуги. Изображение графов.

Определение. Если на плоскости задать конечное множество 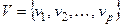точек и конечный набор линий , соединяющих некоторые пары из точек V, то полученная совокупность точек и линий будет называться графом G=G (V, E). Элементы множества V называются вершинами графа, а элементы множества E – ребрами.

Определение. Списком ребер графа называется перечень его ребер с указанием соединяемых вершин.

Определение. Если - ребро графа, то и называются концами ребра.

Определение. Инцидентной ребру называется каждая из концевых вершин этого ребра. Ребро называется инцидентным своим концевым вершинам.

Определение. Смежными называются два ребра, инцидентные одной вершине (имеют общую вершину).

Определение. Смежными называются две вершины, инцидентные одному ребру (имеют общее ребро).

Определение. Ребра, соединяющие одинаковые вершины, называются петлями (на рисунке 1.4 при вершине 5 имеется петля).

Определение. Одинаковые пары в множестве E называются кратными (или параллельными) ребрами. Количество одинаковых пар 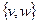в E называется кратностью ребра 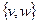. Например, на рисунке 1.1 все рёбра имеют кратность 1, а на рисунке 1.2 есть два ребра, соединяющих одни и те же вершины 1 и 4, следовательно, их кратность равна двум.

Определение. Граф с кратными ребрами – псевдограф.

Определение. Псевдограф без петель называется мультиграфом.

Если в наборе E ни одна пара не встречается более одного раза, то мультиграф называется графом.

Ниже, на рисунке 1.1 изображен граф, на рисунке 1.2 мультиграф, на рисунке 1.4 – псевдограф.

Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины. На рисунке 1 изображены некоторые неориентированные графы.

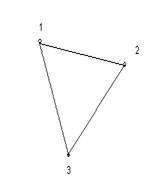
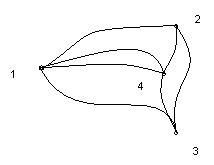
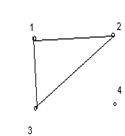
1.1 1.2 1.3

1.4 1.5

Рис. 1

Замечание. Слово “линия”, которое мы используем, подразумевает несущественность того, какая конкретно линия используется для соединения двух вершин графа, то есть её геометрические характеристики не имеют значения.

Определение. Если пары в наборе E являются упорядоченными, то граф называется ориентированным или орграфом.

Если пишут – дуга орграфа, то вершина v – начало, а вершина w – конец дуги е.

Определение. Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется висячей, если ее степень равна единице и изолированной, если ее степень равна нулю.

На рисунке 1.5 все вершины, кроме вершины 1, являются висячими. На рисунке 1.3 вершина 4 является изолированной. Если граф состоит только из таких вершин, его называют пустым. В некоторых случаях пустым называют граф, не имеющей ни одной вершины.

На рисунке 2 представлены различные типы ориентированных графов.

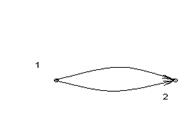
2.1 2.2 2.3

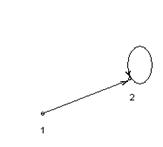
2.4 2.5

Рис. 2

Теорема 1. (теорема Эйлера). Сумма степеней всех вершин графа равна удвоенному числу его рёбер: .

Следствием теоремы Эйлера является Лемма о рукопожатиях – сумма степеней всех вершин графа есть чётное число.

Название леммы интерпретируется так: вершины графа это люди, а ребра – рукопожатия двух людей. При любом числе рукопожатий общее число пожатых рук всегда чётное.

1. Матрица инцидентности. Матрица смежности графа.

Рассмотрим неориентированный граф , имеющий p вершин и q ребер.

Определение. Матрицей смежности вершин 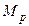неориентированногографа называется квадратная матрица порядка p, элементы которой определяются по правилу:

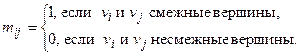
Индексы независимо друг от друга.

Например, матрицей смежности графа рис. 3

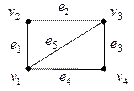
Рис.3

является квадратная матрица четвертого порядка .

Определение. Матрицей инцидентности 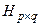неориентированногографа называется матрица размерности p на q, элементы которой определяются по правилу:

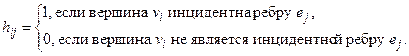
Например, матрицей инцидентности графа рис.3 является матрица размерности четыре на пять

.

Для ориентированного графа матрицы смежности и инцидентности составляется иначе.

Определение. Матрицей смежности 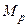ориентированногографа называется квадратная матрица порядка p, элементы которой определяются по правилу:

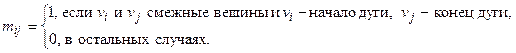
Индексы независимо друг от друга.

Например, матрицей смежности узлов графа рис.4

Рис.4

является квадратная матрица четвертого порядка .

Определение. Матрицей инцидентности 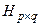ориентированногографа называется матрица размерности p на q, элементы которой определяются по правилу:

Например, матрицей инцидентности графа рис.4 является матрица

.

Дата добавления: 2015-10-13