Свойства минимальных путей в нагруженном ориентированном графе

Нагруженные графы

Нагруженный граф − ориентированный граф D=(V,X), на множестве дуг которого определена некоторая функция 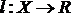, которую называют весовой функцией.

Цифра над дугой (см. рис. 5)− вес дуги (цена дуги).

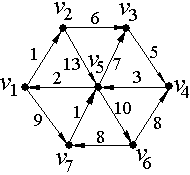
Рис. 5.

Обозначения: для любого пути П нагруженного ориентированного графа D через l(П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П).

Величина l называется длиной пути.

Если выбрать веса равными 1, то придем к ненагруженному графу.

Путь в нагруженном ориентированном графе из вершины v в вершину w, где v¹w, называется минимальным, если он имеет наименьшую длину.

Аналогично определяется минимальный путь в нагруженном графе.

Введем матрицу длин дуг C(D)=[cij] порядка n, причем

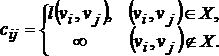
Свойства минимальных путей в нагруженном ориентированном графе

1) Если для " дуги 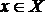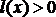то " минимальный путь (маршрут) является простой цепью;

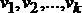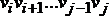2) если минимальный путь (маршрут) то для " i,j: путь (маршрут) тоже является минимальным;

3) если 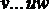− минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k+1 дуг (ребер), то минимальный путь (маршрут) из v в u среди путей (маршрутов), содержащих не более k дуг (ребер).

Алгоритм Форда.

Максимальная пропускная способность графа.

Рассмотрим алгоритм Форда на примере графа изображенного на рис.1. Допустим, у нас исток будет в 1 узле, а сток в 4 узле. Алгоритм можно разбить на три шага: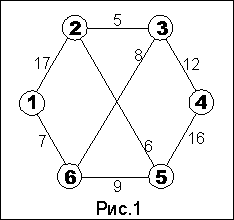

Поиск произвольного пути из истока к стоку. Если такого нет, то выдаем значение максимальной пропускной способности и алгоритм завершается.

Нахождение в выбранном пути ребра с минимальной пропускной способностью. Прибавляем значение этого ребра к пропускной способности, которая в начале выполнения алгоритма равна 0.

Вычитание из всех значений ребер пути, значения минимального ребра этого пути. При этом само ребро обратиться в 0 и его уже нельзя учитывать в дальнейшем. Далее продолжаем с шага 1.

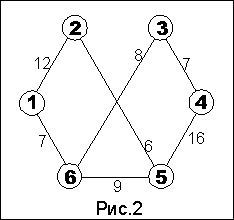
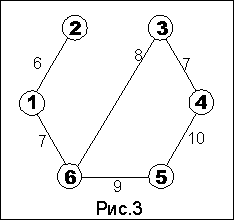
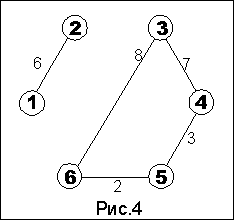
В начале у нас пропускная способность равна 0 (P=0).Допустим, мы нашли путь из истока 1 в сток 4 через вершины 2 и 3, т.е. весь путь можно записать как (1-2-3-4). В этом пути минимальное ребро соединяет вершины 2 и 3, его значение 5, увеличиваем пропускную способность на 5 (Р=5). Вычитаем 5 из ребер соединяющих вершины 1 и 2, 2 и 3, 3 и 4. Из исходного графа у нас выпало ребро соединяющее вершины 2 и 3. Получился граф изображенный на рис.2. В этом графе снова ищем произвольный путь из 1 в 4. Нашли (1-2-5-4), где минимальное ребро соединяет 2 и 5, его значение 6. Увеличиваем пропускную способность на 6 (P=5+6=11). Вычитаем 6 из всех ребер пути, выпадает ребро 2-5 (рис.3). На следующем шаге находим путь (1-6-5-4), минимальное ребро 1-6 равно 7, тогда P=11+7=18. Вычитаем из ребер пути 6, при этом выпадает ребро 1-6 и граф распадается на две компоненты рис.4. Мы не находим пути из истока в сток и алгоритм завершается. Получаем максимальную пропускную способность из 18.

Дата добавления: 2015-10-13