|
Читайте также: |
Определение. Назовём орграф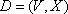 
нагруженным, если на множестве дуг X определена некоторая функция 
которую часто называют весовой функцией.
Тем самым и нагруженном орграфе D каждой дуге 
поставлено в соответствие некоторое действительное число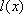 
Значение 
будем называть длиной дуги X.
Для любого пути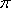 
нагруженного орграфа D обозначим через 
сумму длин входящих в 
дуг, при этом каждая дуга учитывается столько раз, сколько она входит в путь. Величину будем называть длиной пути в нагруженном орграфе D. Ранее так называлось количество дуг в пути В связи с этим заметим, что если длины дуг выбраны равными 1, то 
выражает введенную ранее длину пути в ненагруженном орграфе.
Следовательно, любой ненагруженный орграф можно считать нагруженным с длинами дуг, равными. Аналогично определяется и нагруженный граф, а также длина маршрута в нем.
Дата добавления: 2015-10-13; просмотров: 93 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства минимальных путей в нагруженном ориентированном графе | | | Творчі та теоретико-практичні завдання |