
Читайте также:
|
ПРОГРАММА ЭКЗАМЕНА
зимняя сессия, 2012/2013 уч.год.
Лектор: доц. Синчуков А.В.
1. Расширение понятия определенного интеграла на случаи некомпактных промежутков и неограниченных функций. Несобственные интегралы и их свойства. Исследование сходимости интегралов  .
.
2. Необходимое и достаточное условие сходимости несобственного интеграла от неотрицательной функции. Исследовать сходимость интеграла  .
.
3. Абсолютно сходящиеся несобственные интегралы. Исследовать интеграл на абсолютную сходимость 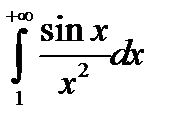 .
.
4. Понятие числового ряда и его суммы. Примеры. Геометрическая прогрессия. Пользуясь определением, исследовать сходимость ряда  .
.
5. Сходящиеся и расходящиеся числовые ряды. Простейшие свойства сходящихся рядов: умножение на константу и сумма сходящихся рядов. Необходимое условие сходимости ряда. Пользуясь необходимым условием, решить вопрос о сходимости ряда 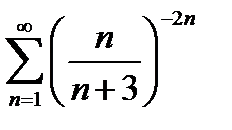 .
.
6. Критерий Коши сходимости числовой последовательности и числового ряда. С С помощью критерия Коши исследовать сходимость гармонического ряда 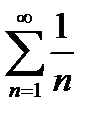 .
.
7. Сходимость рядов с неотрицательными членами. Необходимое и достаточное условие сходимости ряда с неотрицательными членами. Проиллюстрировать на примере ряда  .
.
8. Признак сравнения сходимости рядов с неотрицательными членами. Проиллюстрировать на примерах: 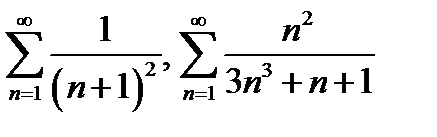 .
. 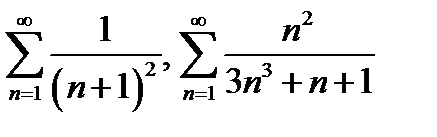
9. Признак Д’Аламбера сходимости рядов. Проиллюстрировать на примерах:  .
.
10. Признак Коши сходимости рядов. Проиллюстрировать на примерах:  .
.
11. Интегральный признак сходимости. Исследование сходимости рядов  .
.
12. Знакочередующиеся ряды. Признак Лейбница. Проиллюстрировать на примере ряда 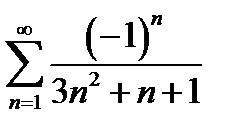 .
.
13. Абсолютно сходящиеся ряды и их свойства. Теоремы о перестановке членов абсолютно сходящегося ряда.
14. Функциональные последовательности и ряды. Сходимость и равномерная сходимость функциональных последовательностей и рядов. Область сходимости. Исследовать на поточечную и равномерную сходимость последовательность  на множествах
на множествах  .
.
15. Необходимое и достаточное условие равномерной сходимости функциональной последовательности. Проиллюстрировать на примере последовательности  .
.
16. Признак Вейерштрасса равномерной сходимости функциональных рядов. Проиллюстрировать на примере ряда  .
.
17. Непрерывность предела равномерно сходящейся последовательности и суммы равномерно сходящегося ряда непрерывных функций. Доказать непрерывность функции  .
.
18. Интегрирование равномерно сходящихся функциональных последовательностей и рядов.
19. Дифференцирование равномерно сходящихся функциональных последовательностей и рядов.
20. Определение степенного ряда. Теорема Абеля. Радиус и интервал сходимости степенного ряда.
21. Свойства степенных рядов.
22. Условия разложения функции в степенной ряд. Ряды Тейлора.
23. Разложение в ряд Тейлора основных элементарных функций.
24. Определение тригонометрического ряда и ряда Фурье. Формулы для коэффициентов ряда Фурье. Теорема о разложении в ряд Фурье кусочно-гладкой функции.
25. Примеры разложения функций в ряд Фурье. Неполные ряды Фурье.
26. Понятие метрического пространства. Примеры. Пространство  .
.
27. Пространство R n. Расстояние между точками в пространстве R n. Неравенство Коши-Буняковского.
28. Окрестности точек. Открытые множества и их свойства.
29. Замкнутые множества и их свойства.
30. Определение предела последовательности в метрическом пространстве. Свойства предела.
31. Связь предела последовательности в R n с пределами ее координатных последовательностей. Теорема Больцано-Вейерштрасса в R n.
32. Компактные множества. Критерий компактности в пространстве R n.
33. Функции нескольких переменных. График. Линии уровня. Примеры.
34. Определение и свойства предела и непрерывности функции нескольких переменных.
35. Теорема об ограниченности непрерывной функции на компактном множестве.
36. Теорема о наибольшем и наименьшем значениях непрерывной функции.
37. Теорема о промежуточном значении непрерывной функции.
38. Равномерная непрерывность функции нескольких переменных. Теорема Кантора.
39. Определение частных производных функции нескольких переменных. Примеры.
40. Определение дифференцируемости функции нескольких переменных. Необходимое условие дифференцируемости.
41. Непрерывность дифференцируемой функции.
42. Достаточное условие дифференцируемости.
43. Дифференцирование композиции.
44. Дифференциал и его геометрический смысл.
ЛИТЕРАТУРА
1. Кудрявцев Л.Д. Курс математического анализа, т.1,2,3. – М.: Дрофа, 2003-2006.
2. Архипов Г.И., В.А. Садовничий, Чубариков В.Н. Лекции по математическому анализу. – М: Дрофа, 2004.
3. Зорич В.А. Математический анализ, т.1,2. – М.: МЦНМО, 2007.
4. Фихтенгольц Г.М. Основы математического анализа, т.1,2. – СПб.: Лань, 2006.
5. Никольский С.М. Курс математического анализа. – М.: Физматлит, 2001.
Дата добавления: 2015-10-13; просмотров: 95 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Раздел XIV. ЗАКЛЮЧИТЕЛЬНЫЕ ПОЛОЖЕНИЯ | | | Образовательных организаций города Курска |