Решение. 1.Проверить наличие аномальных наблюдений.

1.Проверить наличие аномальных наблюдений.

Для выявления аномальных уровней временного ряда используем метод Ирвина:

l_t = |y_t - y_t-1|/S_y

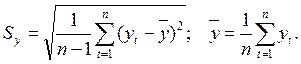
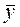= 14,67; S_y = 7,52

t	y(t)	y(t) – y(t-1)	λt
		–	–
			0,53
			0,4
			0,13
			0,53
			0,27
			0,53
			0,53
			0,27

Рассчитанные величины λ_t не превышают табличных значений критерия Ирвина: λ_табл=1,5, следовательно, аномальных наблюдений нет.

2.Построим линейную модель.

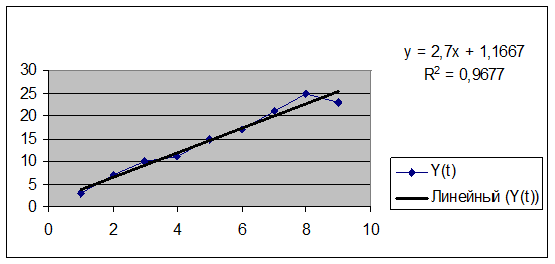
Построим линейную однопараметрическую модель регрессии Y(t). Для этого воспользуемся MS Excel и встроенными функциями. Результат регрессионного анализа представлен в таблице.

	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	1,166666667	1,049187138	1,111971949
t	2,7	0,186445447	14,48144774

Оценим параметры модели «вручную». Промежуточные расчеты параметров линейной модели приведены в таблице:

	t	y(t)	t-tср	(t-tср)^2	y(t) - y(t)ср	(t-tср)*(y(t) - y(t)ср)
			-4		-11,67	46,68
			-3		-7,67	23,01
			-2		-4,67	9,34
			-1		-3,67	3,67
					0,33
					2,33	2,33
					6,33	12,66
					10,33	30,99
					8,33	33,32
Сумма
Ср.зн.		14,67

Рассчитаем параметры линейной модели.

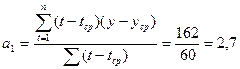
а₀ = y(t)ср- а₁*tср = 14,67-2,7*5 = 1,17

Получим, Y=1,17+2,7*t. Т.е. при вычислении «вручную» получаем те же результаты.

3.Оценим адекватность построенной модели.

а) проверку случайности уровней остаточной компоненты проводим на основе критерия поворотных точек. Значение случайной переменной считается поворотной точкой, если оно одновременно больше или меньше соседних с ним элементов. Для этого каждый уровень ряда сравним с двумя соседними.

t	Отклон. Е(t)	Точ.пов.	Е(t)^2	[E(t)-E(t-1)]^2	Е(t)*Е(t-1)	|E(t)/y(t)|
	-0,867		0,7511			0,289
	0,433		0,1878	1,69	-0,3756	0,062
	0,733		0,5378	0,09	0,3178	0,073
	-0,967		0,9344	2,89	-0,7089	0,088
	0,333		0,1111	1,69	-0,3222	0,022
	-0,367		0,1344	0,49	-0,1222	0,021
	0,933		0,8711	1,69	-0,3422	0,044
	2,233		4,9878	1,69	2,0844	0,089
	-2,467		6,0844	22,09	-5,5089	0,107

Общее число поворотных точек р = 5. В случайном ряду чисел должно выполняться строгое неравенство: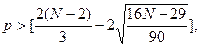

[2*(9-2)/3-2√(16*9-29)/90] = [2,7] = 2.

5>2 – неравенство выполняется, следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.

б) при проверке независимости опре­деляется отсутствие в ряду остатков систематической состав­ляющей с помощью d-критерия Дарбина—Уотсона: 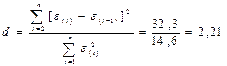d`= 4 – 2,21=1,79

Сравним полученное значение с табличным. Решение попадает в интервал от d₂ до 2, значит, гипотеза о независимости уровней остаточной последовательности, т.е. ряд остатков не коррелирован и модель адекватна по данному признаку.

в) соответствие ряда остатков нормальному закону распределения определим с помощью RS-критерия.

RS= [ε_max – ε_min]:S_ε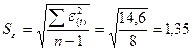

RS = [2,2+2,5]:1,35 = 3,5

Расчетное значение RS попадает в интервал (2,7<3,479<3,7), следовательно, выполняется свойство нормальности распределения. Модель по этому критерию адекватна.

4.Оценим точность модели на основе использования средней относительной ошибки аппроксимации.

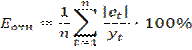
t	y(t)	E(t)	|E(t)|/y(t)
		-0,867	0,289
		0,433	0,062
		0,733	0,073
		-0,967	0,088
		0,333	0,022
		-0,367	0,021
		0,933	0,044
		2,233	0,089
		-2,467	0,107
Сумма			0,795

Е_отн = 0,795/9*100% = 8,83 %

Ошибка не превосходит 15% модель можно считать приемлемой по точности.

5.По построенной модели осуществим прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 70%). Для вычисления точечного прогноза в построенную модель подставляем соответствующее значение:

Y=1,167+2,7*t

Y=1,167+2,7*10=28,167 – на 10-ую неделю;

Y=1,167+2,7*11=30,867 – на 11-ую неделю.

Для учета случайных колебаний при прогнозировании рассчитаем доверительные интервалы: Примем значение уровня значимости α = 0,3 следовательно, доверительная вероятность равна 70%, а критерий Стьюдента при v = п — 2 = 7 равен 1,12. Ширину доверительного интервала вычислим по формуле:

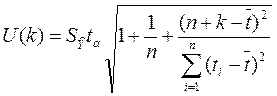, где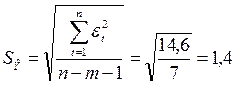

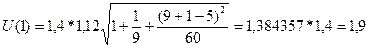
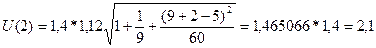
Далее, вычисляем верхнюю и нижнюю границы прогноза. Получили интервальный прогноз:

п + к	U(k)	Прогноз	Формула	Верхняя граница	Нижняя граница
	U(l) = 1,9 U (2) = 2,1	28,2 30,9	Прогноз + U(1) Прогноз - U (2)	30,1 33,0	26,3 28,8

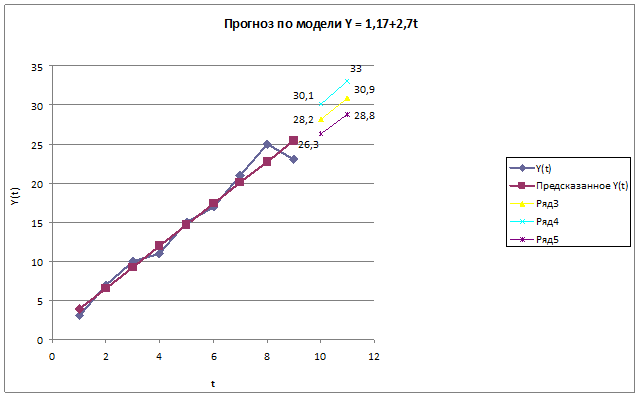
6.Фактические значения показателя, результаты моделирования и прогнозирования представим графически.

---

Дата добавления: 2015-10-13