Решение

Задача 1.3

Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется, по меньшей мере, 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный – 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум, и почему?

Решение

Составим экономико-математическую модель. Для этого обозначим число наборов удобрений: через x₁ – обычный, черезx₂ – улучшенный наборы. Тогда, целевая функция будет иметь вид:

f (x) =3 x₁ +4 x₂→ min

Ограничения:

3х₁ +2х₂ ≥ 10 – по количеству азота,

4х₁ + 6х₂ ≥ 20 – по количеству фосфора,

х₁ + 3х₂ ≥ 7 – по количеству калия,

х₁≥0

х₂ ≥0

Строим область допустимых решений:

1) 3х₁ +2х₂ = 10

x₁ = 0, x₂ = 5

x₁ = 2, x₂ = 2

3*0+2*0<10 – следовательно, решением неравенства является полуплоскость выше прямой.

2) 4х₁ + 6х₂ = 20

x₁ = 2, x₂ = 2;

x₁ = 5, x₂ = 0.

4*0+6*0<20 – следовательно, решением неравенства является полуплоскость выше прямой.

3) х₁ + 3х₂ = 7

x₁ = 1, x₂ = 2

x₁ = 7, x₂ = 0

1*0+3*0<7 – следовательно, решением неравенства является полуплоскость выше прямой.

Пересечением всех плоскостей является неограниченная область (заштрихованная область на графике).

Для определения направления движения к оптимуму построим вектор-градиент, соединив начало координат с точкой с координатами (3;4). Построим линию уровня. Она перпендикулярна вектору- градиенту.

Перемещаем линию уровня в направлении, противоположенном вектору-градиенту до тех пор, пока она не покинет пределов области допустимых решений. Крайняя точка области допустимых решений при этом движении является точка с координатами (2;2) – она и есть точка минимума.

Найдем ее координаты путем решения системы уравнений:

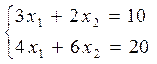
х₁= 2; х₂=2.

Значение целевой функции в точке с координатами (2;2) равно:

min f (x) = 3*2+4*2 = 14

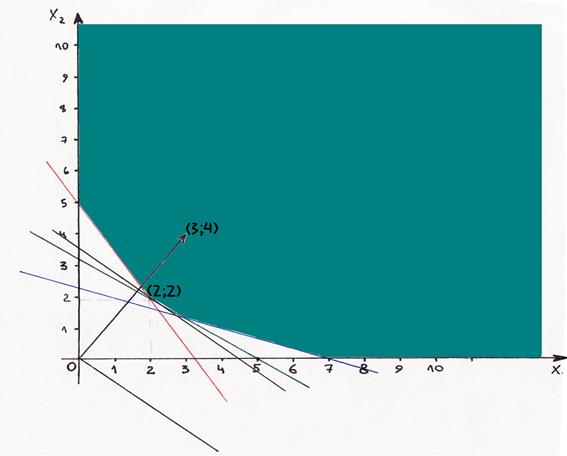
Ответ: чтобы обеспечить эффективное питание почвы и минимизировать стоимость необходимо купить 2 обычных набора и 2 улучшенных набора. Стоимость при этом будет составлять 14 денежных единиц. Если решать данную задачу на максимум, то она не будет иметь решения, так как область допустимых решений не ограничена сверху.

Дата добавления: 2015-10-13