Решение. 1.Сформулируем экономико-математическую модель задачи

1.Сформулируем экономико-математическую модель задачи. Обозначим через x₁, x₂, x₃, x₄ количество продукции каждого типа. Тогда, целевая функция будет иметь вид: f (x) = 5 x₁ + 7 x₂ + 3 x₃ + 6 x₄ → max.

Ограничения:

2 x₁ + x₂ + 3 x₃ + 2 x₄ ≤ 200

x₁ + 2x₂ + 4 x₃ + 8x₄ ≤160

2 x₁ + 4 x₂ + x₃ + x₄ ≤170

x₁, x₂, x₃ , x₄ ≥0

Найдем оптимальное решение с помощью EXCEL. Введем исходные данные и ограничения:

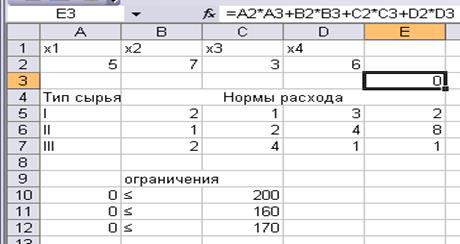
Воспользуемся командой Поиск решения. Заполним окно Поиск решения:

В окне Поиск решения нажать на кнопку Выполнить. В диалоговом окне Результаты поиска решения нажать ОК. В результате:

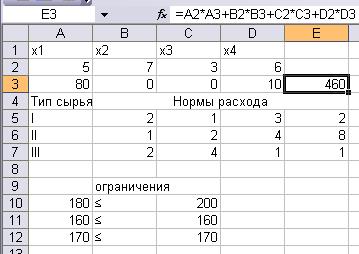
Полученное решение означает, что максимальный доход 460 единиц можно получить при выпуске 80 изделий А и 10 изделий Г. При этом сырье II и III типа будет использовано полностью, а из 200 единиц сырья I типа будет использовано 180 единиц. Изделия Б и В убыточны, затраты на ресурсы превышают цену изготовления из них изделий.

2.Сформулируем двойственную задачу и найдем ее оптимальный план.

Число неизвестных в двойственной задаче равно числу ограничений в исходной задаче. Следовательно, в двойственной задаче 3 неизвестных: y₁, y₂, y₃.

Целевая функция двойственной задачи формулируется на минимум. Коэффициенты при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи:

g (y) = 200 y₁ +160 y₂ +170 y₃→ min

Необходимо найти такие цены на сырье, чтобы общая стоимость сырья была минимальной.

Число ограничений в двойственной задаче равно числу переменных в исходной задаче. В исходной задаче 4 переменных, значит, в двойственной задаче 4 ограничения. В правых частях ограничений двойственной задачи стоят коэффициенты при неизвестных в целевой функции исходной задачи. Левая часть ограничений определяет стоимость ресурсов, затраченных на производство единицы изделия:

2 y₁ + y₂ +2 y₃ ≥ 5

y₁ +2 y₂ +4 y₃ ≥ 7

3 y₁ +4 y₂ + y₃ ≥ 3

2 y₁ +8 y₂ + y₃ ≥ 6

y₁, y₂, y₃ ≥0

Найдем оптимальный план двойственной задачи, используя теоремы двойственности.

Согласно второй теореме двойственности тем значениям х, которые больше 0, соответствуют строгие равенства в ограничениях двойственной задачи. Получим систему:

2 y₁ + y₂ +2 y₃ = 5 0 + y₂ + 2 y₃ = 5

2 y₁ +8 y₂ + y₃ = 6 0 + 8 y₂ + y₃ = 6

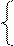y3 = 34/15

y2 = 7/15

Подставим в систему, получим y₁ =0. Подставим значения y в целевую функцию.

200 * 0 + 160 * 7/15 + 170 * 34/15 = 460.

Поскольку значения целевых функций в исходной и двойственной задачах одинаковы – решения верны.

3. Сырье типа I используется не полностью, поэтому имеет нулевую двойственную оценку (y₁ = 0).Нулевая оценка ресурса свидетельствует о его недефицитности, которая возникла из-за невозможности его полного использования в оптимальном плане. Этот ресурс не влияет на план выпуска продукции. Данный ресурс не препятствует и дальше максимизировать целевую функцию.

4.На основе свойств двойственных оценок и теорем двойственности:

· если изделие вошло в оптимальный план, то в двойственных оценках оно не убыточно, т.е. стоимость сырья, затраченного на производство изделия, равна его цене. Такие изделия выгодны с точки зрения принятого критерия оптимальности. В задаче — это изделия A и Г. Если стоимость ресурсов, затраченных на производство одного изделия, больше его цены, то это изделие не войдет в оптимальный план из-за его убыточности. В задаче в план выпуска не вошли изделия Б и В, потому что затраты по ним превышают цену.Сырье II и III имеют отличные от нуля оценк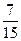и и 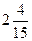- эти ресурсы полностью используются в оптимальном плане и являются дефицитными, т.е. сдерживающими рост целевой функции. Правые части этих ограничений равны левым частям.

· определим, как изменятся общая стоимость продукции и план ее выпуска при увеличении запасов сырья I и II видов на 8 и 10 ед. соответственно и уменьшении на 5 ед. запасов сырья III вида:

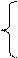
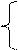
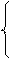x1 + 2x2 + 4x3 + 8x4 = 160+10, x1 +8x₄ =170, х4 = 35/3,

2х1 +4x2 ++ x3 + х₄ = 170 – 5. 2x1 + x4 = 165. x1 = 230/3

Значение целевой функции: 453,3.

460-453,3=6,7

Следовательно, выручка уменьшилась на 6,7 ден.ед.

· определим целесообразность включения в план изделия «Д» ценой 10 ден. ед., на изготовление которого расходуется по две единицы каждого вида сырья. Вычислим ∆ = 2*0 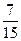+ 2* +2* 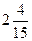-10 = - 3 < 0, т.е. затраты на производство данного изделия не превышают его цену, следовательно, включать такое изделие в план выгодно.

Дата добавления: 2015-10-13