
|
Читайте также: |
Министерство образования и науки
Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
РЕШЕНИЕ ТИПОВОГО ВАРИАНТА ИНДИВИДУАЛЬНОГО ДОМАШНЕГО ЗАДАНИЯ ПО ТЕМЕ
«МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Для студентов 2 курса всех направлений
Волгодонск 2013
УДК 519.22 (076.5)
Ф 947
Рецензент д.т.н., проф. Сысоев Ю.С.
Составители Алексеева М.А., Чабанова Н.И., Гладун К.К.
Решение типового варианта индивидуально домашнего задания по теме «Математическая статистика»./ М.А. Алексеева, Н.И. Чабанова, К.К. Гладун. – ВИТИ НИЯУ МИФИ. – Волгодонск, 2013. – 20 с.
Предназначено для студентов 2-го курса всех направлений.
© ВИТИ НИЯУ МИФИ, 2013
Предисловие.
В целях лучшего усвоения курса и интенсификации самостоятельной работы студентов в соответствии с учебными планами Волгодонского инженерно-технического института (филиала) НИЯУ МИФИ предусмотрено выполнение индивидуальных домашних заданий (ИДЗ).
Данный дидактический материал предназначен для организации самостоятельной работы студентов, выполняющих индивидуальные домашние задания по теме «Математическая статистика».
Задание 1. В результате эксперимента получены данные в виде статистического ряда.
а) записать значения результатов эксперимента в виде вариационного ряда;
б) найти размах варьирования и разбить его на 5 интервалов;
в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
г) найти числовые характеристики выборки 
д) приняв в качестве гипотезы: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при уровне значимости 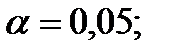
е) найти доверительный интервал для математического ожидания и среднего квадратического отклонения при надежности 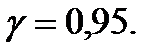
Решение. Пусть для изучения количественного признака Х (например, размер детали) из генеральной совокупности извлечена выборка объема n =50.
Наблюдавшиеся значения х1 ; х2;…; хn называются вариантами.
Значения вариант хi приведены в табл. 1:
Таблица 1
| Варианты хi | |||||||||
| 19.8 | 16.3 | 12.0 | 10.0 | 11.2 | 13.4 | 17.6 | 18.0 | 20.0 | 10.9 |
| 14.7 | 15.3 | 12.7 | 18.1 | 19.4 | 12.1 | 13.6 | 15.4 | 19.6 | 18.0 |
| 16.3 | 12.7 | 15.4 | 13.0 | 11.7 | 14.6 | 17.5 | 16.7 | 15.0 | 18.7 |
| 11.1 | 13.4 | 17.5 | 18.9 | 20.0 | 10.0 | 17.7 | 18.1 | 12.7 | 13.4 |
| 14.6 | 12.4 | 18.3 | 16.2 | 17.0 | 14.2 | 15.3 | 11.8 | 15.7 | 19.9 |
а) Расположим все варианты от 10.0 до 20.0 в порядке возрастания и получим вариационный ряд (табл. 2).
Таблица 2
| Вариационный ряд | |||||||||
| 10.0 | 10.0 | 10.9 | 11.1 | 11.2 | 11.7 | 11.8 | 12.0 | 12.1 | 12.4 |
| 12.7 | 12.7 | 13.0 | 13.4 | 13.4 | 13.4 | 13.6 | 14.2 | 14.6 | 14.6 |
| 14.7 | 15.0 | 15.3 | 15.3 | 15.4 | 15.4 | 15.7 | 16.2 | 16.3 | 16.3 |
| 16.7 | 17.0 | 17.5 | 17.5 | 17.6 | 17.7 | 18.0 | 18.0 | 18.0 | 18.1 |
| 18.1 | 18.3 | 18.7 | 18.9 | 19.4 | 19.6 | 19.8 | 19.9 | 20.0 | 20.0 |
б) Частичных интервалов 
Разобьем все значения от 10.0 до 20.0 на 5 интервалов:
[10.0 – 12.0), [12.0 – 14.0), [14.0 – 16.0), [16.0 – 18.0), [18.0 – 20.0].
Зададим статистическое распределение выборки в виде последовательности интервалов и соответствующих им частот. В качестве частоты интервала принимают количество вариант, попавших в интервал.
Размах 
Сумма частот 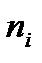 вариант
вариант  должна быть равна объему выборки
должна быть равна объему выборки 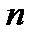 ; длина частичного интервала (шаг)
; длина частичного интервала (шаг) 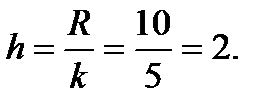
Полученная табл. 3 является статистическим распределением выборки.
Таблица 3
| № интервала i | Частичные интервалы xi – xi+1 | Сумма частот вариант интервала ni |
| 10.0 – 12.0 | ||
| 12.0 – 14.0 | ||
| 14.0 – 16.0 | ||
| 16.0 – 18.0 | ||
| 18.0 – 20.0 |
Найдем относительные частоты 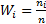 и плотность относительной частоты
и плотность относительной частоты 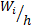 (табл. 4). Контроль:
(табл. 4). Контроль: 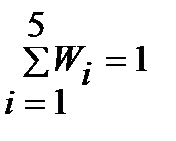 .
.
Таблица 4
| Частоты | Относительные частоты | Плотность относит. частоты |
| ni | 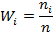
| 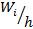
|
 =0.14 =0.14
| 0.07 | |
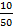 =0.2 =0.2
| 0.1 | |
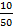 =0.2 =0.2
| 0.1 | |
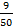 =0.18 =0.18
| 0.09 | |
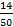 =0.28 =0.28
| 0.14 |
в) Построим гистограмму частот и относительных частот по данному распределению выборки объема n =50 (рис. 1).
На оси абсцисс отложим частичные интервалы длиной h=2.
На оси ординат отложим плотность относительной частоты 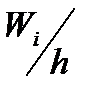 . Проведем над частичными интервалами отрезки, параллельные оси абсцисс, на расстоянии, соответствующем плотности относительной частоты
. Проведем над частичными интервалами отрезки, параллельные оси абсцисс, на расстоянии, соответствующем плотности относительной частоты  .
.
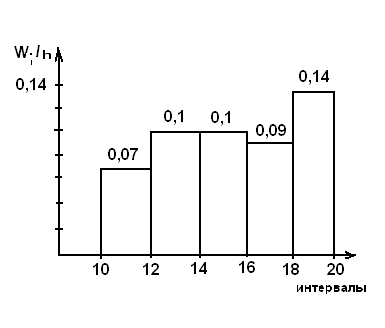
Рис. 1
Построим полигон частот. Примем середины интервалов в качестве новых вариант  и составим статистическое распределение выборки (табл.5).
и составим статистическое распределение выборки (табл.5).
Таблица 5

| |||||
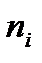
|
На оси абсцисс отложен вариант  , на оси ординат частоты
, на оси ординат частоты 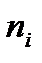 . Соединим точки
. Соединим точки 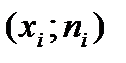 отрезками. Полученная ломаная и есть полигон частот (рис.2).
отрезками. Полученная ломаная и есть полигон частот (рис.2).
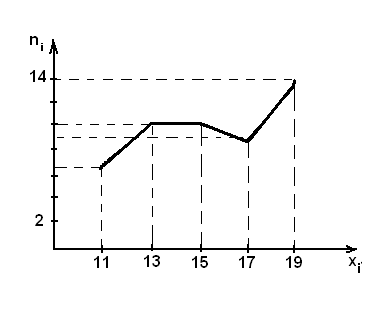
Рис. 2
Эмпирическая функция распределения:

График функции 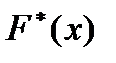 изображен на рисунке 3.
изображен на рисунке 3.
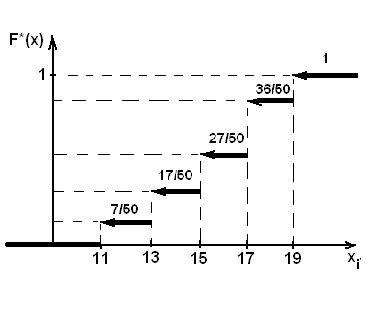
Рис. 3
г) Вычислим выборочную среднюю  где
где  - варианта,
- варианта, 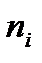 - частота,
- частота, 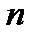 - объем выборки. Данные возьмем в табл.5.
- объем выборки. Данные возьмем в табл.5.
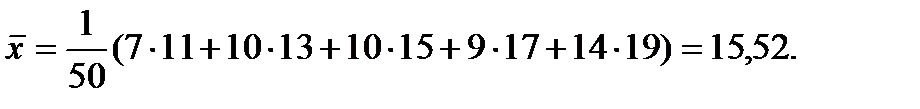
Вычислим выборочную дисперсию:

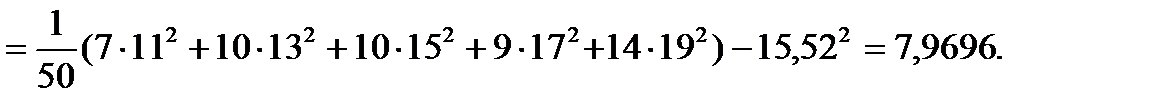 Для уменьшения ошибки, вызванной малым числом интервалов, сделаем поправку Шеппарда, тогда выборочная дисперсия
Для уменьшения ошибки, вызванной малым числом интервалов, сделаем поправку Шеппарда, тогда выборочная дисперсия
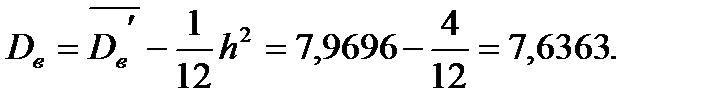
Вычислим выборочное среднее квадратическое отклонение:

Найдем несмещенную оценку генеральной дисперсии:
«исправленная» выборочная дисперсия
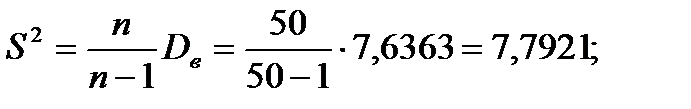
«исправленное» среднее квадратическое отклонение
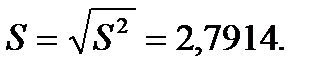
д) По критерию согласия Пирсона проверим, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объема n =50, где выборочное среднее 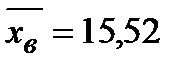 , выборочное среднее квадратическое отклонение
, выборочное среднее квадратическое отклонение 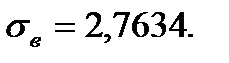 Уровень значимости
Уровень значимости 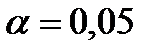 – это вероятность отвергнуть правильную гипотезу.
– это вероятность отвергнуть правильную гипотезу.
Найдем интервалы 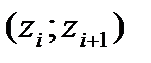 . Для этого составим расчетную таблицу 6. Левый конец первого интервала примем за
. Для этого составим расчетную таблицу 6. Левый конец первого интервала примем за
–∞, правый конец последнего интервала примем за +∞.
Таблица 6
| Границы | Границы | |||||

| 
| 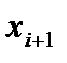
| 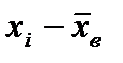
| 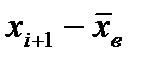
| 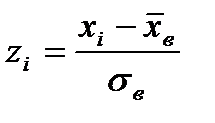
| 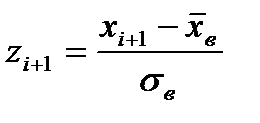
|
| 10.0 | 12.0 | -- | -3.52 | –∞ | -1.2738 | |
| 12.0 | 14.0 | -3.52 | -1.52 | -1.2738 | -0.5500 | |
| 14.0 | 16.0 | -1.52 | 0.48 | -0.5500 | 0.1737 | |
| 16.0 | 18.0 | 0.48 | 2.48 | 0.1737 | 0.8974 | |
| 18.0 | 20.0 | 2.48 | -- | 0.8974 | +∞ |
Найдем теоретические вероятности Pi и теоретические частоты ni´= n· Pi = 50 · Pi. Для этого составим расчетную таблицу 7. Значения функции Ф(х) находятся в таблицах, причем Ф(–∞) =-1/2, Ф(+∞)-1/2, Ф(–х) = –Ф(х).
Таблица 7
| Границы | Значения | Теор.вероят. | Частоты | |||
| i | zi | zi+1 | Ф(zi) | Ф (zi+1) | Pi= Ф (zi+1)– Ф (zi) | ni´ =50 Pi |
| –∞ | -1.2738 | -0.5 | -0.3980 | 0.1021 | 5.1 | |
| -1.2738 | -0.5500 | -0.3980 | -0.2080 | 0.1892 | 9.46 | |
| -0.5500 | 0.1737 | -0.2080 | 0.0675 | 0.2763 | 13.815 | |
| 0.1737 | 0.8974 | 0.0675 | 0.3133 | 0.2458 | 12.42 | |
| 0.8974 | +∞ | 0.3133 | 0.5 | 0.1867 | 9.205 |
Сравним эмпирические и теоретические частоты, используя критерий Пирсона. Для этого составим расчетную таблицу 8. Столбцы 7 и 8 служат для контроля.
Таблица 8
| Номер столбца | |||||||

| 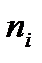
| 
| 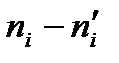
| 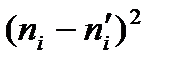
| 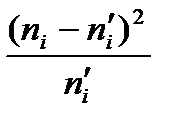
| 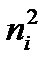
| 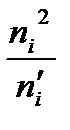
|
| 5.1 | 1.9 | 3.61 | 0.7078 | 9.6078 | |||
| 9.46 | 0.54 | 0.2916 | 0.0308 | 10.5708 | |||
| 13.815 | -3.815 | 14.5542 | 1.0535 | 7.2385 | |||
| 12.42 | -3.42 | 11.6964 | 0.9417 | 6.5217 | |||
| 9.205 | 4.795 | 22.9920 | 2.4978 | 21.2928 | |||
| Σ | χ2набл =5.2316 | 55.2316 |
Наблюдаемое значение критерия: 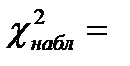
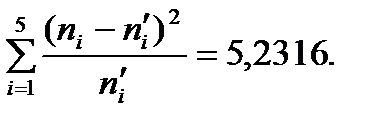
Контроль:  – верно.
– верно.
По таблице критических точек 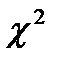 , по уровню значимости α = 0,05 и числу степеней свободы k = S – 3 = 5– 3 = 2, где S – число интервалов, находим критическую точку правосторонней критической области: χ2кр(0.05;2) = 6.
, по уровню значимости α = 0,05 и числу степеней свободы k = S – 3 = 5– 3 = 2, где S – число интервалов, находим критическую точку правосторонней критической области: χ2кр(0.05;2) = 6.
Так как χ2набл =5.2316< χ2кр = 6, то нет основания отвергать гипотезу о нормальном распределении генеральной совокупности, то есть эмпирические и теоретические частоты различаются незначимо.
е) Найдем интервальные оценки.
Доверительный интервал с надежностью γ = 0,95 для неизвестного математического ожидания а нормально распределенного признака генеральной совокупности, если известно генеральное среднее квадратическое отклонение σ = 3, выборочное среднее x в = 15.52, объем выборки n =50:
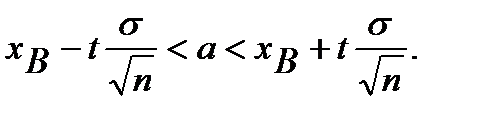
Найдем t из соотношения 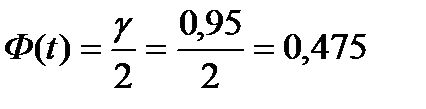 . Из таблиц функции Ф(x) находим аргумент t= 1,96, тогда доверительный интервал для математического ожидания:
. Из таблиц функции Ф(x) находим аргумент t= 1,96, тогда доверительный интервал для математического ожидания:
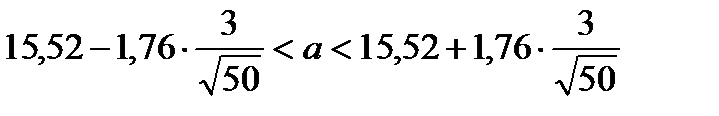 ;
;
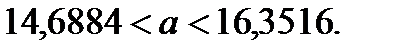
Доверительный интервал с надежностью γ = 0,95 для среднего квадратического отклонения σ нормально распределенного признака генеральной совокупности по «исправленному» выборочному среднему квадратическому отклонению S= 2,7914.
При q < 1 – это доверительный интервал S(1– q) < σ < S(1+ q).
При q > –1 доверительный интервал 0 < σ < S(1+ q), где q находят по таблице: q(γ;n)= q( 0,95;50 )= 0.21<1.
Итак, доверительный интервал для среднего квадратического отклонения:
2.7914·(1–0.21) < σ < 2.7914·(1+0.21),
2.2052 < σ < 3.3776.
Задание 2. Проведены 20 независимых опытов по изучению зависимости случайных величин X и Y (таблица 9).
а) построить график зависимости (поле корреляции) между переменными X и Y, по которому найти модель уравнения регрессии;
б) рассчитать параметры уравнения регрессии методом наименьших квадратов (МНК);
в) оценить тесноту связи между переменными с помощью показателей корреляции и детерминации:
г) оценить значимость коэффициентов корреляции и регрессии по критерию Стьюдента при уровне значимости 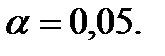
Таблица 9
| X | -10 | -8 | -6 | -4 | -2 | |||||
| Y | -2,6 | -3,2 | -2,3 | -2,0 | 2,3 | -0,5 | 4,0 | 5,9 | 5,3 | 6,7 |
| X | ||||||||||
| Y | 5,4 | 9,6 | 10,3 | 11,7 | 12,2 | 13,4 | 10,5 | 11,4 | 14,5 | 17,8 |
Решение.
а) В прямоугольной системе координат строим график зависимости переменных X и Y (рис.4). Для удобства выделим по пять интервалов изменения этих переменных, используя формулы:
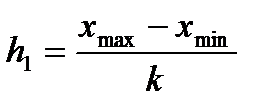 и
и 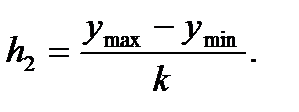
Для переменной Х получим: 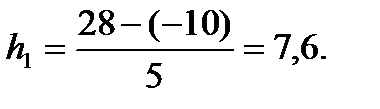
Длину интервала округлим в сторону увеличения, т.е. положим 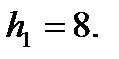 В результате получим следующие границы интервалов:
В результате получим следующие границы интервалов:
-10; -2; 6; 14; 22; 30.
Аналогичные расчеты производим для переменной Y:
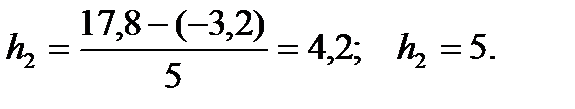
Границы интервалов составят:
-4; 1; 6; 11; 16; 21.
На график наносим точки 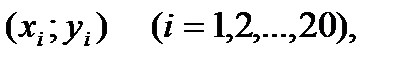 координаты которых соответствуют значениям переменных X и Y.
координаты которых соответствуют значениям переменных X и Y.
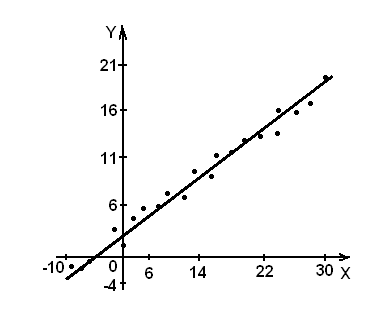
Рис.4
Визуально анализируя характер расположения точек на графике (рис.4), приходим к выводу, что связь между переменными X и Y может быть выражена линейным уравнением регрессии 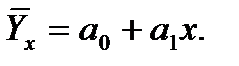
б) Параметры уравнения регрессии находим методом наименьших квадратов, путем составления и решения системы нормальных уравнений:
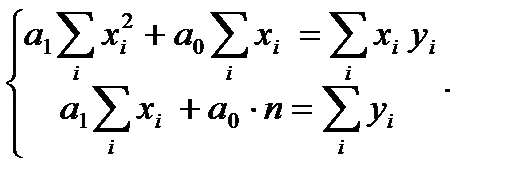
Составим расчетную таблицу 10.
Таблица 10
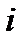
| 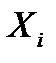
| 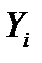
| 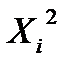
| 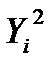
| 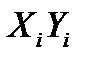
|
| -10 | -2,6 | 6,76 | 26,0 | ||
| -8 | -3,2 | 10,24 | 25,6 | ||
| -6 | -2,3 | 5,29 | 13,8 | ||
| -4 | -2,0 | 4,00 | 8,0 | ||
| -2 | 2,3 | 5,29 | -4,6 | ||
| -0,5 | 0,25 | 0,0 | |||
| 4,0 | 16,00 | 8,0 | |||
| 5,9 | 34,81 | 23,6 | |||
| 5,3 | 28,09 | 31,8 | |||
| 6,7 | 44,89 | 53,6 | |||
| 5,4 | 29,16 | 54,0 | |||
| 9,6 | 92,16 | 115,2 | |||
| 10,3 | 106,09 | 144,2 | |||
| 11,7 | 136,89 | 187,2 | |||
| 12,8 | 163,84 | 230,4 | |||
| 13,4 | 179,56 | 268,0 | |||
| 10,5 | 110,25 | 231,0 | |||
| 11,4 | 129,96 | 273,6 | |||
| 14,5 | 210,25 | 377,0 | |||
| 17,8 | 316,84 | 498,4 | |||

| 1630,62 | 2564,8 |
Тогда система примет вид:
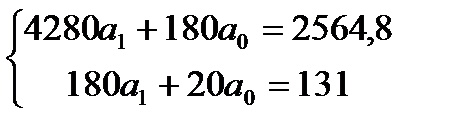
Решим систему по формулам Камера:
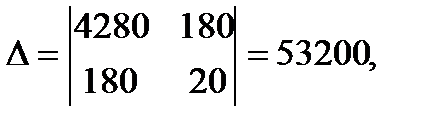
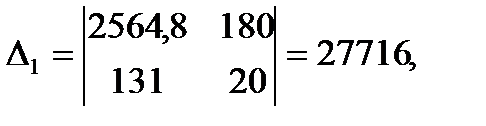
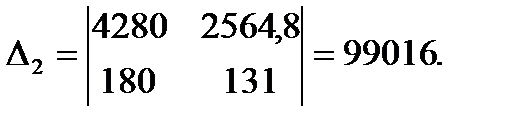
Следовательно, 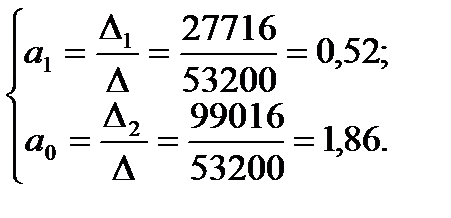
Таким образом, уравнение регрессии Y на X имеет вид:
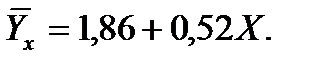
Построим линию регрессии Y на X по таблице:
| X | -3,57 | |
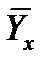
| 1,86 |
Линия регрессии изображена на рисунке 4.
в) При линейной зависимости степень тесноты связи между X и Y определяется с помощью коэффициента корреляции:
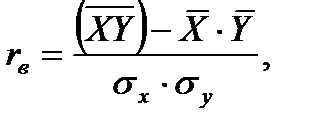
где средние арифметические значения:
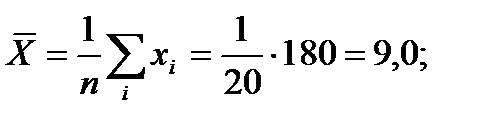
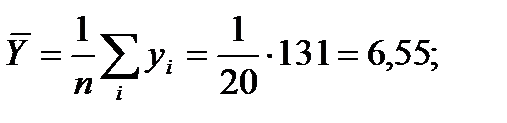
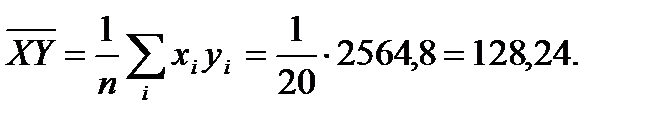
Найдем:
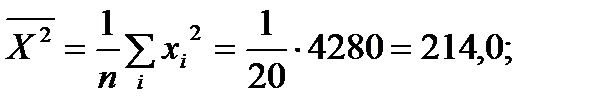

Вычислим средние квадратические отклонения  и
и  :
:
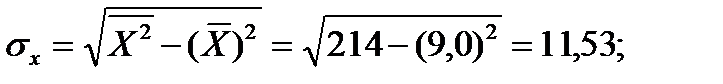
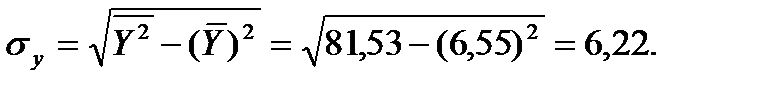
Отсюда, 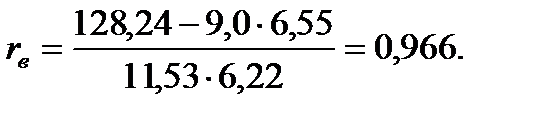
Т.к.  то между признаками связь очень тесная, близкая к линейной функциональной.
то между признаками связь очень тесная, близкая к линейной функциональной.
Коэффициент детерминации равен 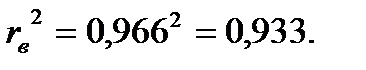
г) Оценить значимость коэффициента корреляции.
Нулевая гипотеза 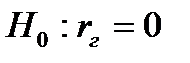 - переменная X не оказывает существенного влияния на Y.
- переменная X не оказывает существенного влияния на Y.
Конкурирующая гипотеза 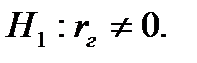
Для проверки нулевой гипотезы применим критерий Стьюдента. Уровень значимости 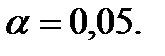 Коэффициент корреляции
Коэффициент корреляции 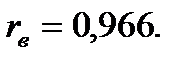 Найдем наблюдаемое значение критерия:
Найдем наблюдаемое значение критерия:
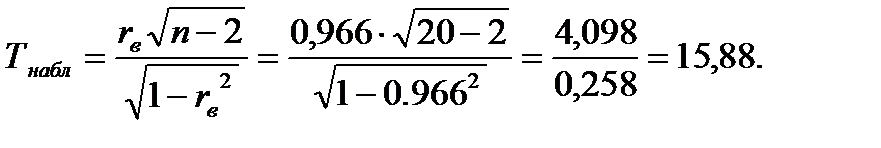
По таблице критических точек распределения Стьюдента по уровню значимости 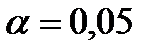 и числу степеней свободы
и числу степеней свободы 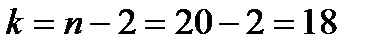 найдем критическую точку:
найдем критическую точку:
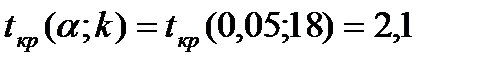 двусторонней критической области.
двусторонней критической области.
Т.к. 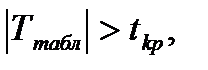 то нулевую гипотезу отвергаем.
то нулевую гипотезу отвергаем.
Вывод: выборочный коэффициент корреляции значим, случайные величины X и Y коррелированы.
Задача 3. Известно, что между X и Y существует линейная корреляционная зависимость (табл.11).
а) найти уравнение прямой регрессии;
б) построить уравнение эмпирической линии регрессии и случайные точки выборки.
Таблица 11
| X\Y | 2,3, | 3,8 | 5,3 | 6,8 | 8,3 | 9,8 | 11,3 | 12,8 | 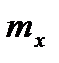
|
| - | - | - | - | - | |||||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | |||||
| - | - | - | - | - | |||||
| - | - | - | - | - | |||||
| - | - | - | - | - | - | ||||
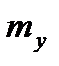
| 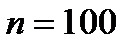
|
а) Уравнение прямой регрессии Y на X имеет вид:
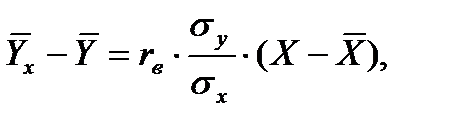
где 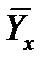 - условная средняя;
- условная средняя;
 и
и 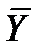 - выборочные средние признаков X и Y;
- выборочные средние признаков X и Y;
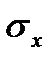 и
и 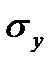 - выборочные средние квадратичные отклонения;
- выборочные средние квадратичные отклонения;
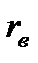 - выборочный коэффициент корреляции.
- выборочный коэффициент корреляции.
Найдем выборочные средние  и
и 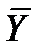 . (Целые числа внутри таблицы являются кратностями значений соответствующих случайных точек):
. (Целые числа внутри таблицы являются кратностями значений соответствующих случайных точек):
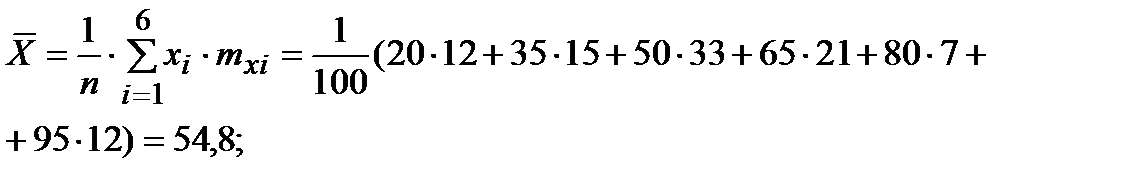
 Определим средние арифметические значения
Определим средние арифметические значения  ,
, 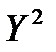 и
и  :
: 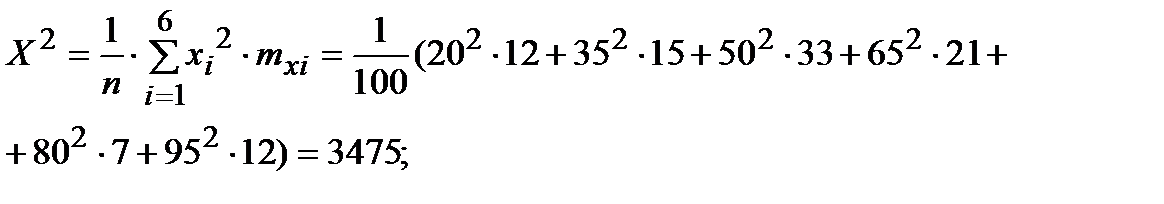


Определим дисперсию и ковариацию.
Дисперсии: 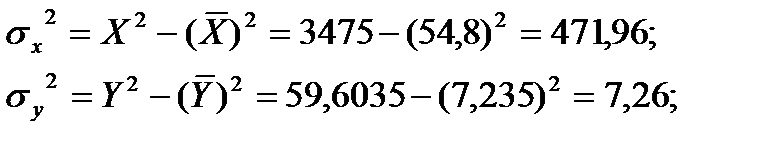
Ковариация: 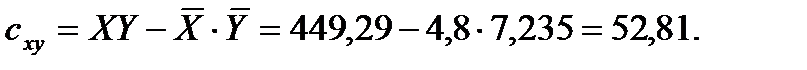 Находим
Находим 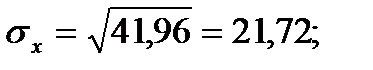 и
и 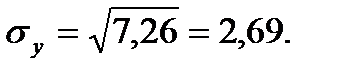
Определим коэффициент корреляции:
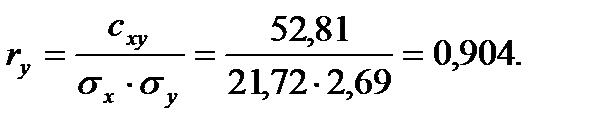
Вычислим значение произведения:
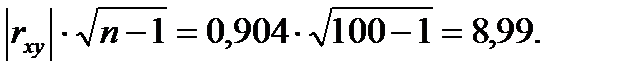
Т.к. 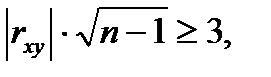 то связь достаточно вероятна.
то связь достаточно вероятна.
Уравнение прямой регрессии Y на X:
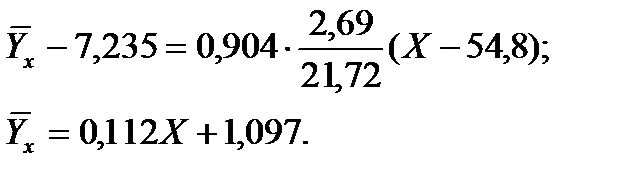
б) Построим линию регрессии по двум точкам:
| X | -9,79 | |
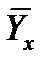
| 1,097 |
и случайные точки выборки (рис. 5).

Рис.5
Дата добавления: 2015-10-13; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПРИЛОЖЕНИЕ № 7. Образец заполнения Заявления на отмену Авторизации | | | Критерії психічного здоров`я. |