Лабораторна робота №1

Тема: Рішення транспортних задач методом нелінійного програмування шляхом використання похідних.

Мета роботи: отримати теоретичні знання і практичні навики з рішення транспортних задач на екстремум.

Завдання №1. (задача на максимум)

Є прямокутний лист жерсті (рис.1.) зі сторонами АВ і ВС. Необхідно виготовити з цього листа відкриту зверху коробку для зберігання металевої стружки з максимальним об’ємом шляхом вирізання біля всіх кутів квадратиків і згортання кромок. Дані для індивідуальних завдань наведені в таблиці №1. Номер індивідуального завдання визначається порядковим номером студента у журналі.

Задача на максимум

Дано прямокутний лист жерсті зі сторонами , 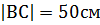. Потрібно вирізати біля всіх кутів рівні квадратики (рис.1.), так, щоб після згортання кромок, що залишились, вийшла відкрита зверху коробка для стружки максимальної ємності.

Розв’язання:

Позначивши через х довжину сторони квадратика, що вирізається, складемо рівняння для визначення об’єму коробки:

V (х)= х (80 – 2 х)(50 – 2 х) (1)

Запишемо цільову функцію максимуму об’єму коробки:

х (80 – 2 х)(50 – 2 х) max (2)

Знайдемо похідну функції V (х):

V’ (х)= =12 (3)

Прирівнюємо V’ (х) до нуля, знаходимо критичні точки:

12 =0 (4)

Очевидно, що аргумент х може змінюватись в наступних межах:

.

Тому при зміні величини х від 0 до 25см функція (3) має тільки одну екстремальну точку х =10. Це точка максимуму, оскільки V’ (х) при . Звідси слідує, що функція V (х) досягає максимального значення при х =10.

Максимальний об’єм коробки становить:

= .

Рис.1. Вид прямокутного листа жерсті.

таблиця№1 (довжина сторін прямокутника, см)

№ варіанту	АВ	ВС

Завдання №2. (задача на мінімум)

На прямій АВ проходить залізниця (рис.1). В стороні від неї на відстані l знаходиться пункт С ( l, CD _|_ AB). Потрібно з пункту С перевезти вантаж в пункт, що знаходиться на залізниці в напрямку А на відстані R від D (Відстань R досить велика). Визначити в яку точку М злізниці більш вигідно перевезти вантаж автомобілями з пункту С, щоб потім його відправити по залізниці, якщо вартість перевезення однієї тони вантажу на відстань 1км автомобільним транспортом в m разів дорожче ніж залізницею (m )?

Розв’язання:

Позначивши через х відстань , визначимо величину – відстань на перевезення вантажу до залізниці:

(1)

Тоді по залізниці залишиться проїхати відстань R – x (звертаємоувагу на те, що ми розглядаємо невід’ємні значення величини R – x).

Також відмітимо, що везти вантаж в точку 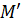розташовану лівіше точки D не доцільно. Дійсно, перевезення вантажу в будь – яку точку залізниці, розташовану правіше точки D на відстані не більше , більш вигідно (див.рис.1).

Позначимо через у сумарну вартість перевезень (залізницею і автомобільним транспортом). Вона буде пропорційна сумі:

(2)

Знайдемо при якому значенні х ( R) сумарна вартість досягає мінімального значення.

Похідна функції у дорівнює:

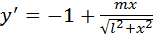(3)

Знайдемо критичні точки функції (3) при

або .

Можна відмітити, що:

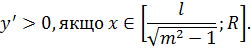
Тому – точка мінімуму функції 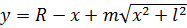на [0;R].

В цій же точці функція у досягає свого мінімального значення.

Таким чином, найвигіднішим буде перевезення вантажу до залізниці під кутом 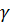, котангенс якого дорівнює:

,(див.рис.1).

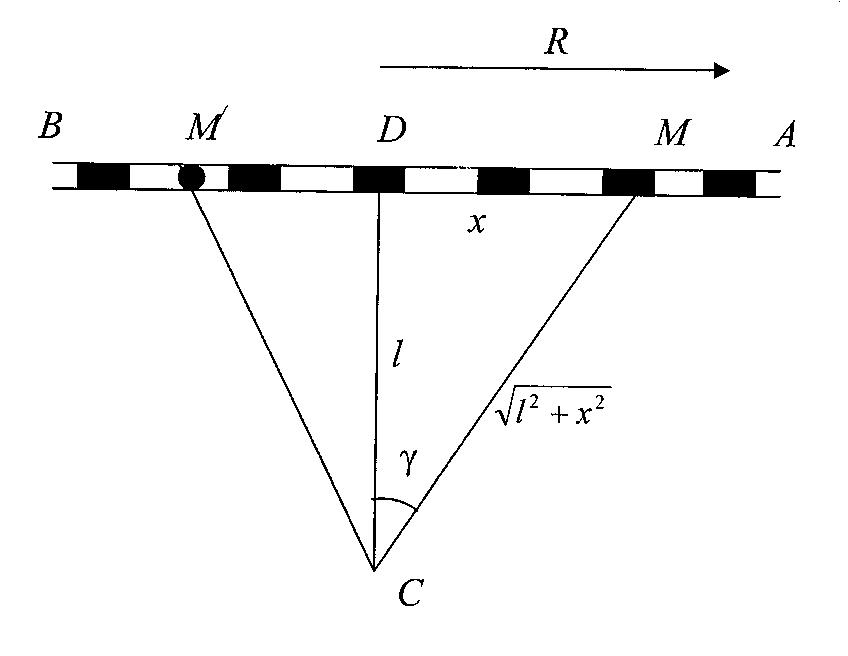
Рис.2. Схема перевезення вантажу автомобільним транспортом і залізницею.

таблиця№2

№ варіанту	значення показників
l,км	m
		2.0
		2.1
		2.2
		2.3
		2.4
		2.5
		2.6
		2.7
		2.8
		2.9
		3.0
		2.0
		2.1
		2.2
		2.3
		2.4
		2.5
		2.6
		2.7
		2.8
		2.9
		3.0
		2.0
		2.1
		2.2
		2.3

Дата добавления: 2015-10-13