Футрин А.И.

Типовой расчёт по физики №4

Тема: «Электрическое поле в вакууме».

Выполнил:

студент группы АС 34:

Футрин А.И.

Проверил:

Борушко В.В

Брест 2011г.

Вариант 82

Дано:

R1=

R2

q1=

q2=

Решение: Рисунок (вариант 15):

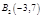
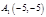
Задание 1:

 

   

Обозначим за расстояние от точки О до точки С. - размеры, заряд бесконечно малой части стержня.

Проведем аналогичные вычисления для напряженности вдоль оси O y:

Поскольку формулы, полученные в результате интегрирования, подходят и для другого стержня, как и для других точек, найдем значения напряженностей ():

Для второго стержня до точки С ():

Для второго стержня до точки D ():

Нетрудно видеть, что векторы вдоль оси О y компенсируют друг друга, то есть, .

Задание 2:

Задание 3:

Рассмотрим, какие элементы системы создают электрическое поле в точке . Для этого нарисуем рисунок:

Обозначим за напряженность в точке, которую создает стержень 1;

- напряженность, которую создает стержень 2;

- напряженность, которую создает точечный заряд ;

- напряженность, которую создает точечный заряд ;

- напряженность, создаваемая диском.

Как известно, напряженность, создаваемая зарядами в какой-либо точке, равна векторной сумме всех напряженностей в данной точке:

.

Поскольку в предыдущих заданиях мы находили проекции векторов напряженности на соответствующе оси, будем последовательно находить напряженность в данной точке:

Поскольку суммы соответствующих проекций векторов будут равны проекциям результирующего вектора суммы, найдем эти проекции (заметим, что нужно учитывать направление вектора):

Нарисуем такой же рисунок для точки (оставим те же обозначения, что и в предыдущем пункте):

Выпишем проекции соответствующих векторов:

Учитывая направление, найдем проекции результирующего вектора и его длину:

Задание 4:

Поскольку в задании 2 мы уже нашли потенциалы поля в двух данных точках, то подставим полученные значения в выражение и посчитаем ответ:

Таким образом, мы нашли разность потенциалов для электрического поля системы.

Задание 5:

Поскольку , тогда имеем:

Сравним результаты, полученные в задании 4. Обратим внимание на то, что результаты равны ().

Задание 6:

Так как , тогда имеем:

Заметим, что данные, полученные в результате подсчетов, приблизительно равны данным, полученным в предыдущих заданиях, что свидетельствует о том, что задание выполнено верно.

Дата добавления: 2015-10-13