Различные виды уравнения прямой.

Рассмотрим прямую проходящую через точки М1М2, пусть М произвольная точка лежащая на этой прямой тогда векторы ММ2 и М1М являются коллинеарными. Вектор ММ2 = (X2 – X; Y2 – Y), M1M = (X - X1; Y – Y1). Из условия коллинеарности векторов, следует, что 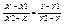1). 1) -уравнение прямой, проходящей через две заданные точки пусть X2 – X1 = K, Y2 – Y1 = L, тогда вектор a = (K; L) параллельна данной прямой направляющий вектор 1) может быть записано в виде: 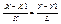2). 2) -уравнением прямой проходящей через данную точку М1 в заданном направлении 2) каноническим уравнением прямой. Если три точки М1, М2 и М лежат на одной прямой, то площадь треугольника равна нулю. 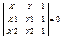3). 3) – уравнение прямой в виде определителя приравняем отношение равенства 1) к некоторому числу T. X - X1 = (X2 – X) T, X –X1 = KT; Y – Y1 = (Y2 –Y1) T, Y – Y1 = LT. (X = X1 + KT, Y = Y1 + LT 4)). 4) – называется параметрическим уравнением. Пусть на плоскости заданы две точки A и B, лежащие на координатных осях A(a; 0), B(b; 0). Найдем уравнение прямой проходящей через точки A и B. 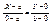; ; 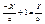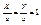- 5). 5) – называется уравнением прямой на отрезке.

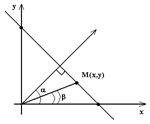
Нормальное уравнение прямой. Пусть прямаяпроходит через точку М(X; Y) перпендикулярно отрезку OP. Длина отрезка 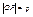, , 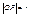cos 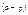, p = r(cosacos + sinasinb), p = (r cosb)cosa + (r sinb)sina. X cosa + Y sinb = p – нормальное уравнение прямой.

Дата добавления: 2015-09-07