Отметим свойства вероятности

Свойство 1. Если все случаи являются благоприятствующими данному событию 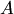, то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления , так как в этом случае :

Свойство 2. Если нет ни одного случая, благоприятствующего данному событию 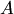, то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления , так как в этом случае :

Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.

Свойство 4. Вероятность наступления противоположного события определяется так же, как и вероятность наступления, события :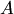

где — число случаев, благоприятствующих появлению противоположного события . Отсюда вероятность наступления противоположного события равна разнице между единицей и вероятностью наступления события :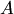

5. Статистическое определение ТВ - Вероятностью случайного события называется число, около которого группируются частоты этого события по мере увеличения числа испытаний.

6. Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

Сумма событий обозначается так:

7. Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Произведение событий обозначается

8. Противоположное с. – соб. состоящее в не наступлении события А, называется ему противоположным и обозначается А

9. Теоремы сложения вероятностей:

- Вероятность сумм 2х несовместных событий А и В = сумме их вероятностей

Р(А+В)=Р(А)+Р(В)

- Вероятность суммы несколько попарно совместных событий А1, А2….Аn = сумме их вероятностей

Р(А1, А2…Аn)=Р(А1)+Р(А2)+…Р(Аn)

- Сумма вероятностей событий Р (А)+Р(А) = 1

10. Вероятность события В вычисляется при условии, что событие А наступило, называется условием вероятности события В и обозначается Р(В/А)

11. Теоремы умножения вероятностей.

- Вероятность произведения 2х событий А и В = вероятности событий А на условии вероятности события В, вычисляется при условии, что событие А наступило.

Р (АВ)= РА) Р(В/А)

- Р (А1A2…An)= Р(А1)Р(А2/А1)Р(А3/А1А2)…(Аn/А1А2….Аn-1)

12. 2 события называются не зависимыми, если наступление одного из них не изменят вероятность наступления другого, в противном случае события называются зависимыми.

13. Дискретной называется случайная величина, принимающая конечное или бесконечное счетное множество значений. Например: частота попаданий при трех выстрелах; число бракованных изделий в партии из штук; число вызовов, поступающих на телефонную станцию в течение суток; число отказов элементов прибора за определенный промежуток времени при испытании его на надежность; число выстрелов до первого попадания в цель и т. д.

14. Законом распределения случайной величины называется соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения.

15. Математическое ожидание дискретной случайной величины Х называется сумма произведения всех возможных значений хi этой величины, на соответствующие им. вероятности

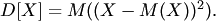16. В качестве меры рассеивания случайной величины используют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, которое называют дисперсией случайной величины и обозначают :

С помощью дисперсии и среднеквадратического отклонения можно судить о рассеивании случайной величины вокруг математического ожидания.

17. Размерность дисперсии равна квадрату размерности случайной величины и поэтому ее нельзя интерпретировать геометрически. Этих недостатков лишено среднее квадратическое отклонение случайной величины, которое вычисляется по формуле

18. Случайную величину будем называть непрерывной, если ее интегральная функция распределения { < } непрерывна и дифференцируема, за исключением, быть может, конечного числа точек.

Время работы прибора.

19. Плотность распределения вероятностей непрерывной случайной величины называется функция вероятностей того, что в результате испытания НСВ Х примет значение из интервала ∆х

20. Св-ва f(x)

-

-

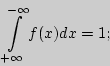- Условия нормировки

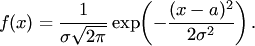21. Случайная величина называется нормально распределенной с параметрами а и σ, если ее плотность вероятностей имеет вид:

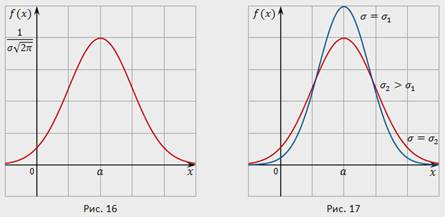
график плотности распределения вероятностей в случае нормального распределения

22. вероятность попадания в интервал в случае нормального распределения

P(x₁<x<x₂) Ф (x₂-а/σ) – Ф(x₁-а/σ)

23. Правило трёх сигм () — практически все значения нормально распределённой случайной величины лежат в интервале

Дата добавления: 2015-09-07