Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Вероятность произведения двух событий А и В равна произведению вероятности одного из них (А) на условную вероятность другого (В), вычисленную при условии, что первое имело место.

Читайте также:
  1. A. Под транзитивной зависимостью понимают зависимость одного атрибута от другого через третий атрибут
  2. Auf dem Laufenden sein(a, e) s быть в курсе событий. Syn.: auf dem Laufenden bleiben(ie, ie) s; im Bilde sein über Akk.
  3. III Архангельского международного туристского форума
  4. А тут ведь вполне можно положить еще одного
  5. А) Первое обращение: анамнез.
  6. Большинство хороших фильмов переносят нас в такие места и ситуации, где мы сами не смогли бы оказаться, а лучшие из них глубоко проникают в суть описываемых событий и явлений.
  7. В1951 г. в СССР был создан Олимпийский комитет, признанный МОК, после чего наша страна стала пол­ноправным членом международного олимпийского движения.

Символически это записывается следующим образом:

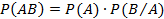
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.

Следствие 2. Вероятность произведения независимых событий равна произведению вероятностей этих событий.

Как уже говорилось, под произведением событий понимается совместное их появление.

Для двух событий по теореме умножения имеем:

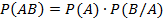
Но поскольку события независимы, справедливо равенство Р(В/А) = Р(В), и тогда получаем: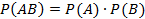

Для трех событий по аналогии получаем: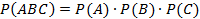

Пример. Из урны, в которой находятся 1 черный и 2 белых шара ( 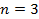), выбираем два шара подряд. Какова вероятность того, что оба шара белые?

Решение. Обозначим интересующее нас событие через А, а события, заключающиеся в выборе белого шара первый и второй раз — через A1 и А2, соответственно. Интересующее нас событие равно произведению событий A1 и А2: .

По теореме умножения имеем: .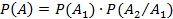

Так как всего шаров три и из них два белых, то .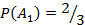

Так как после появления события 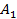(после выбора белого шара первый раз) осталось всего два шара, из них белых – один, то .

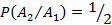Тогда:

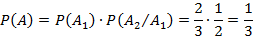
Если после выбора белого шара первый раз его возвращают в урну, то события 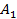и 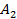будут независимыми и равными:

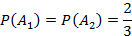
Тогда искомая вероятность будет равна:

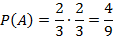
Дата добавления: 2015-09-06; просмотров: 132 | Нарушение авторских прав

Читайте в этой же книге: Невозможному событию приписывается вероятность, равная 0. | Понятия суммы и произведения событий | Пример схемы испытаний Бернулли на конкретном примере |
<== предыдущая страница | следующая страница ==>
Если рассматриваются совместные события, вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности совместного их наступления.| Теорема гипотез и Байесовские подходы.
mybiblioteka.su - 2015-2024 год. (0.011 сек.)