Частные производные и полный дифференциал 1-го порядка

Определение. Производная от функции z=f(x,у) по х, найденная в предложении, что у остается постоянным, называется частной производной от z по х и обозначается или f'_x (x, у). Аналогично определяется и обозначается частная производная z по у.
Если функция z=f(x,у) имеет в точке (х, у) непрерывные частные производные, то ее полное приращение может быть представлено в виде:
, (1)
где при .
Определение. Выражение 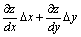является главной частью полного приращения Δ z и называется полным дифференциалом функции z=f(x,у) и обозначается dz:
. (2)
Полагая в формуле (2) z равным х, найдем , а при z=y . Поэтому
. (3)
Из (1) следует, что .
Функция f(x,y) называется дифференцируемой в точке (х,у), если она имеет в этой точке полный дифференциал.
Пример. Найти полный дифференциал функции .
Решение. Сначала найдем частные производные


Производная найдена в предположении, что у постоянна, а найдена в предположении, что х постоянна. По формуле (3):
.
Ответ. dz= (10 x– 6 xy ³) dx +(9 x ² y ²+6) dy.

Дата добавления: 2015-09-06