Метод покоординатного спуска

Рассмотрим функцию двух переменных. Ее линии постоянного уровня представлены на рис. 10, а минимум лежит в точке . (Напомним, что линией постоянного уровня называется кривая в двумерном сечении пространства параметров (в данном случае в плоскости (х1, х2), значение функции на которой - константа). Простейшим методом поиска является метод покоординатного спуска. Из точки А мы производим поиск минимума вдоль направления оси х₁ и, таким образом, находим точку B, в которой касательная к линии постоянного уровня параллельна оси x₁. Затем, производя поиск из точки B в направлении оси x₂, получаем точку C, производя поиск параллельно оси x₁, получаем точку D, и т.д. Таким образом, мы приходим к оптимальной точке. Любой из одномерных методов, описанных в предыдущей главе, может быть использован здесь для поиска вдоль оси. Очевидным образом эту идею можно применить для функций n переменных.

Рис. 10.

Рассмотрим данный метод более детально на примере некоторой целевой функции.

Пусть нужно найти наименьшее значение целевой функции u=f(M)=f(x₁,x₂,...,x_n). Здесь через M обозначена точка n-мерного пространства с координатами x₁,x₂,...,x_n:M=(x₁,x₂,...,x_n). Выберем какую-нибудь начальную точку и рассмотрим функцию f при фиксированных значениях всех переменных, кроме первой: . Тогда она превратится в функцию одной переменной x₁. Изменяя эту переменную, будем двигаться от начальной точки в сторону убывания функции, пока не дойдем до ее минимума при , после которого она начинает возрастать. Точку с координатами обозначим через M¹, при этом .

Фиксируем теперь переменные: и рассмотрим функцию f как функцию одной переменной . Изменяя x₂, будем опять двигаться от начального значения 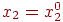в сторону убывания функции, пока не дойдем до минимума при . Точку с координатами обозначим через M², при этом . Проведем такую же минимизацию целевой функции по переменным x₃,x₄,...,x_n. Дойдя до переменной x_n, снова вернемся к x1 и продолжим процесс.

Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек M⁰,M¹,M²,... которой соответствует монотонная последовательность значений функции Обрывая ее на некотором шаге k, можно приближенно принять значение функции f(M^k) за ее наименьшее значение в рассматриваемой области.

Отметим, что данный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Если целевая функция f(x₁,x₂,\ldots,x_n задана явной формулой и является дифференцируемой, то мы можем вычислить ее частные производные и использовать их для определения направления убывания функции по каждой переменной и поиска соответствующих одномерных минимумов.

На рис. 11. изображены линии уровня некоторой функции двух переменных u=f(x,y). Вдоль этих линий функция сохраняет постоянные значения, равные 1, 3, 5, 7, 9. Показана траектория поиска ее наименьшего значения, которое достигается в точке O, с помощью метода покоординатного спуска.

При этом нужно ясно понимать, что рисунок служит только для иллюстрации метода. Когда мы приступаем к решению реальной задачи оптимизации, такого рисунка, содержащего в себе готовый ответ, у нас, конечно, нет.

Рис. 11.

Теоретически данный метод эффективен в случае единственного минимума функции. Но на практике он оказывается слишком медленным. Поэтому были разработаны более сложные методы, использующие больше информации на основании уже полученных значений функции. Было предложено несколько функций, которые из-за своих свойств являются тестовыми для таких методов. Ниже приведено несколько примеров таких функций.

Функция Розенброка:

(4.1)

Функция Пауэлла:

(15)

Двумерная экспоненциальная функция:

Дата добавления: 2015-09-06