Функции нескольких переменных

C. Метод полного перебора (метод сеток).

D. Метод покоординатного спуска.

6. Примеры решения задач в MathCAD.

7. Вопросы и задания.

8. Список рекомендуемых источников.

Функции нескольких переменных

Определение. Переменная z называется функцией переменных х и у, если каждой паре значений х и у в некоторой области их изменения поставлено в соответствие одно значение z. Функциональную зависимость z от х и у записывают в виде: z=f(x,у). Это уравнение определяет некоторую поверхность в пространстве R ³.
Геометрическим образом функции z=x²+y ² является параболоид. Пусть z=a, тогда x ²+ y ²= a, т.е. линия пересечения плоскости z = a с поверхностью z = x ²+ y ² есть окружность x ²+ y ²= a радиуса 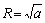. Пусть у =0, тогда z = x ² и, следовательно, при пересечении плоскости O хz с поверхностью получается парабола. Метод сечений дает возможность лучше представить себе геометрический образ данной функции.

Определение. Число А называется пределом функции z=f(x,у) в точке М ₀(х ₀, у ₀), если для каждого числа ε>0 найдется такое число β>0, что для всех точек М (х, у), для которых выполняется неравенство | ММ ₀|<β, будет выполняться неравенство | f (x, у)– A |< ε

Обозначим

.
Определение. Функция z=f(x,у) называется непрерывной в точке М ₀(х ₀, у ₀), если имеет место равенство

.

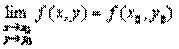Дата добавления: 2015-09-06