Понятие экспертной системы и применение логического вывода при построении экспертных систем.

Экспертной системой (ЭС) называется система, которая позволяет пользователю описать проблемную ситуацию и получить ее решение, сопровождаемое объяснениями, почему выбрано именно это решение.

Перечислим основные компоненты ЭС.

A) ГБД – глобальная база данных (содержит исходную информацию, необходимую для решения проблемной ситуации).

B) БЗ – база знаний, суть набор операции преобразования ГБД (с помощью последовательности этих операций мы и получаем ответ, причем сама последовательность правил составляет определяет обоснование).

C) Стратегия выбора следующей операции.

D) Терминальное состояние ГБД (содержит ответ на вопрос).

Схема работы ЭС выглядит в виде дерева.

//рисунок (17)

Одним из видов ЭС являются ЭС, основанные на предикатных языках представления знаний, и частности на языке ЛППП. В этом случае ГБД представляет собой набор предикатов, а БЗ – суть набор логических формул. Стратегия определяется применяемой стратегией резолюции (например OL-вывод, вывод на клозах Хорна и т.д.) и реализуется с помощью соответствующей машины логического вывода. В случае применения хорновской стратегии, ГБД формулируется в виде хорновских фактов, БЗ – в виде хорновских аксиом, а терминальное состояние в виде хорновской теоремы.

Различают 3 класса запросов к ЭС – классы A, B, C.

2.2.8. Запросы класса A.

Запросы класса A предполагают ответ «да» или «нет». В полноценных системах возможно три случая. Рассмотрим соответствующие примеры.

Пример 1. Предикаты: С(x) – x – человек, S(x) – x – смертен.

ГБД – C(Мао) – Мао человек.

БЗ - "x [C(x) ®S(x)] – все люди смертны

Вопрос. S(Мао) – смертен ли Мао?

Система пытается доказать теорему S(Мао).

C (Мао) ù S (Мао) Ú ù С (Мао) ù S (Мао) Ú ù С (Мао) =

ù С(x) Ú S (x) {Мао/x} С (Мао)

ù S (Мао)

Это удается - ответ «да».

Пример 2. P(x, y) – x в пункте y.

ГБД - P(Иван, Томск) – Иван в Томске.

БЗ - "x [P(x, Томск)®ùP(x, Новосибирск)] – если кто-то в Томске, то он не в Новосибирске.

Вопрос. P(Иван, Новосибирск) – Иван в Новосибирске?

Система пытается доказать теорему P(Иван, Новосибирск).

//вывод (19)

P(Иван, Томск)

ùP (x, Томск) ÚùP (x, Новосибирск) {Иван/x}

ùP (Иван, Новосибирск)

Это невозможно (нет унифицируемых литер).

Система пытается доказать теорему ùP(Иван, Новосибирск)

//вывод (20)

P(Иван, Томск)

ùP (x, Томск) Ú ùP (x, Новосибирск) {Иван / x}

P (Иван, Новосибирск)

P (Иван, Новосибирск)	Ú	ùP(Иван, Томск)
P (Иван, Томск)
P (Иван, Новосибирск)	Ú	ùP(Иван, Томск)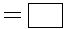

Это удается. Значит, ответ «нет».

Пример 3. ГБД - P(Огород, Бузина) – Бузина в огороде

Вопрос. P(Дядька, Киев) – дядька в Киеве?

Невозможно доказать ни P(Дядька, Киев), ни ùP(Дядька, Киев). Ответ – недостаточно информации (данных или знаний) для получения информации.

Примечание. Иногда автоматизированные системы всегда выдают ответы «да» или «нет» (например, Turbo Prolog в вопросно-ответном режиме). В этом случае ответ «нет» реально может означать, как «нет», так и недостаточность информации.

Дата добавления: 2015-09-06