Проведение эксперимента на модели

Стратегическое планирование эксперимента

Достижение целей моделирования возможно исследованием с использованием созданной модели. Эти исследования заключаются в проведении ряда испытаний, в результате которых определяются выходные характеристики моделируемого объекта при различных значениях управляемых параметров. Эксперименты следует проводить по заранее составленному плану. Существенную важность приобретают вопросы планирования при использовании метода имитационного моделирования. Это обусловлено большим числом сочетаний значений управляемых параметров, а каждый прогон модели проводится при определенном сочетании значений параметров.

При планировании эксперимента в первую очередь определяются управляемые параметры, которые участвуют в эксперименте, так называемые факторы. Выявляются уровни факторов, т.е. значения, которые принимают параметры при проведении испытаний. По возможности следует выбирать минимум уровней и на практике ограничиваются только двумя: нижним и верхним значением соответствующего фактора, условно обозначаемым "-1" и "+1". Если требуется исследовать влияние на отклик n различных факторов, все факторы фиксируют на некоторых уровнях, кроме одного, который изменяется при каждом прогоне модели. В следующей серии прогонов варьируется другой фактор. Последовательная комбинация всех уровней одного фактора со всеми уровнями других дает полный факторный эксперимент. План такого эксперимента для n факторов, варьируемых на двух уровнях, называется планом 2ⁿ. Матрица возможных сочетаний уровней факторов для плана 2³ представлена в табл. 1.

	Таблица 1
Матрица плана 2^n
x1	x2	x3
-1	-1	-1
+1	-1	-1
-1	+1	-1
+1	+1	-1
-1	-1	+1
+1	-1	+1
-1	+1	+1
+1	+1	+1

Зависимость между реакцией системы и уровнями факторов есть факторная функция

y = j (x₁,x₂, x₃),

где x_i - уровень i -го фактора (i = 1…3).

Представляя факторную функцию в виде уравнения регрессии:

для k = 3 получим:

где e - ошибка опыта, которая предполагается независимой нормально распределенной случайной величиной со средним, равным нулю, и постоянной дисперсией.

Для оценки коэффициентов следует использовать план эксперимента 2³. После добавления столбца из +1 и всех столбцов произведений исходных факторов по два и по три получим из исходной матрицы (см.табл.1) матрицу независимых переменных (табл. 2).

Таблица 2
Матрица независимых переменных при полном факторном эксперименте 2^3
x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3
+1	-1	-1	-1	+1	+1	+1	-1
+1	+1	-1	-1	-1	-1	+1	+1
+1	-1	+1	-1	-1	+1	-1	+1
+1	+1	+1	-1	+1	-1	-1	-1
+1	-1	-1	+1	+1	-1	-1	+1
+1	+1	-1	+1	-1	+1	-1	-1
+1	-1	+1	+1	-1	-1	+1	-1
+1	+1	+1	+1	+1	+1	+1	+1

Полный факторный эксперимент может потребовать существенных затрат машинного времени. В теории планирования экспериментов разработаны методы неполных факторных экспериментов. В случае такого эксперимента прогоны модели проводятся для тех опытов, произведения значений трех уровней равны +1. При этом матрица независимых переменных принимает вид (табл.3).

Таблица 3

Матрица независимых переменных при неполном факторном эксперименте 2³

x0	x1	x2	x3
+1	+1	-1	-1
+1	-1	+1	-1
+1	-1	-1	+1
+1	+1	+1	+1

Регрессивные коэффициенты находятся по методу наименьших квадратов:

(1)

где y_i - значение реакции модели в i -м испытании; x_ij - значение j -го уровня в i -м испытании; n - число испытаний.

Тактическое планирование эксперимента

Предпринимается с целью дальнейшего снижения затрат машинного времени при проведении исследований на имитационных моделях при обеспечении достоверности результатов исследований. На этом этапе проводится решение задачи определения необходимого числа реализаций при одном прогоне модели и задачи уменьшения ошибок, обусловленных начальным состоянием модели, отличным от стационарного.

Решение первой задачи состоит в определении необходимого числа реализаций n, обеспечивающего заданную точность и надежность результата. Для вычисления значения n на практике применяются следующие соотношения, устанавливающие зависимость между n, доверительной вероятностью a и доверительным интервалом 2 e искомого параметра:

1) при определении математического ожидания:

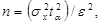
где s _x² - дисперсия случайной величины x; e - величина доверительного интервала; t _a- параметр распределения (наиболее часто встречающиеся пары a и t _a приведены в табл. 4);

Таблица 4
a	0,80	0,85	0,90	0,95	0,99	0,995	0,999
t a	1,28	1,44	1,65	1,98	2,53	2,81	3,30

Для расчета необходимого числа реализаций возьмем доверительную вероятность a= 0,95

Тогда ей соответствует параметр распределения t _a =1,98

2 e - доверительный интервал искомого параметра. Тогда e = 1 - a = 1 – 0,95 = 0,05

Значение для s _x возьмем из листинга испытаний №1 s _x = 106.79

2) при определении вероятности события:

где p - вероятность наступления события.

При расчете возьмем p =0,5

Относительно решения второй задачи следует указать, что большинство имитационных моделей используется для изучения установившихся (стационарных) режимов функционирования исследуемых объектов. Однако в начальный период работы модели (также как и реального объекта) существует переходный режим. Длительность этого режима может быть большой и значения выходных параметров, измеренные в переходный период, смещают их итоговые оценки.

Существуют следующие методы уменьшения таких ошибок:

1) увеличение периода моделирования для нивелирования оценок;

2) инициация модели не с "нулевого", а со специально заданного состояния, близкого к установившемуся;

3) выбор начального момента сбора статистики не с начального момента, а по истечении некоторого времени.

Первый метод приводит к значительному увеличению периода модельных исследований. Второй требует разработки дополнительных аналитических моделей, не лишенных жестких ограничений. Результаты аналитического моделирования используются для установления в имитационной модели параметров стационарного режима. Третий метод основан на знании длительности переходного режима, а это также требует предварительных исследований. Поэтому на практике ограничиваются отсечением начального периода, равного 3-4-кратному времени прохождения модели самыми "медленными" заявками.

Дата добавления: 2015-09-06