
Читайте также:
|
Прямое (декартово) произведение двух групп (G, *) и 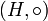 — это группа из всех пар элементов (g, h) с операцией поэлементного умножения:
— это группа из всех пар элементов (g, h) с операцией поэлементного умножения: 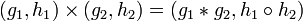 . Эта группа обозначается как
. Эта группа обозначается как 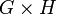 . Сомножители G и H изоморфны двум нормальным подгруппам своего произведения,
. Сомножители G и H изоморфны двум нормальным подгруппам своего произведения, 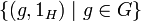 и
и 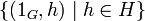 соответственно. Пересечение этих подгрупп состоит из одного элемента (1 G,1 H), который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.
соответственно. Пересечение этих подгрупп состоит из одного элемента (1 G,1 H), который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.
Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.
Однако, для бесконечного числа перемножаемых групп понятия декартового и прямого произведения принято различать. В общем случае, 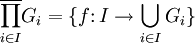 , где
, где 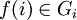 и
и  . (Операция в правой части — это операция группы Gi.) Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп:
. (Операция в правой части — это операция группы Gi.) Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп: 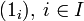 . Например, для счётного числа групп:
. Например, для счётного числа групп: 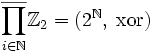 , где в правой части стоит множество всех бесконечных двоичных последовательностей.
, где в правой части стоит множество всех бесконечных двоичных последовательностей.
Подгруппа на множестве всех f, носитель которых (то есть множество 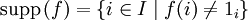 ) конечен, называется прямым произведением. Например, прямое произведение того же самого набора множеств
) конечен, называется прямым произведением. Например, прямое произведение того же самого набора множеств  содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать какдвоичные представления натуральных чисел.
содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать какдвоичные представления натуральных чисел.
Дата добавления: 2015-09-06; просмотров: 129 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПОДСТАНОВКА | | | Прямое произведение топологических пространств |