
|
Читайте также: |
ВВЕДЕНИЕ
В процессе компьютерного или математического моделирования возникают задачи нахождения корней различных алгебраических, тригонометрических и трансцендентных уравнений. Некоторые из них имеют аналитическое решение, другие нет. В общем случае применимы численные методы нахождения корней этих уравнений.
Поскольку при численном решении уравнения f(x)=0 находится за один заход только один корень, то первым шагом в цепочке требуемых действий должно стать нахождение областей изоляции корней, т.е. выделение таких интервалов аргумента, внутри каждого их которых находится корень и причем только один. Наиболее наглядным способом определения этих интервалов является графический: для интересующего диапазона значений аргумента строится график функции f(x). Значения ‘x’ слева и справа от точки пересечения графиком оси абсцисс дадут искомую область изоляции корня: на рис. 1 она лежит между значениями 0,8 и 1,4.
 |
Рисунок 1 – Графический способ выделения области изоляции корня уравнения
Следующий шаг – выбор метода численного решения исходного уравнения. Рассмотрим порядок нахождения корня несколькими часто применяемыми на практике способами.
Метод половинного деления (метод дихотомии)
В этом методе использован тот факт, что значения функции для двух величин аргумента из области изоляции корня: большего и меньшего, чем значение корня – имеют разные знаки. Будем последовательно делить область изоляции корня пополам и выбирать ту ее часть, на краях которой функция принимает значения с противоположными знаками. Выбранный интервал является новой областью изоляции корня. Когда этот интервал станет меньше наперед заданной величины, можно сказать, что корень с требуемой точностью определен. Метод обеспечивает высокую точность нахождения корня, но требует достаточно большого числа шагов.
Порядок расчета таков: для начальной области изоляции корня [a;b] вычисляется первое приближение к корню
x1=  .
.
Находим значение функции в этих точках, т.е. f(a), f(b), f(x1). Если f(a)* f(x1)<0 или
f(b)* f(x1)>0, то новой областью изоляции корня будет [a;x1]. В этом случае второе приближение к корню
x2=  .
.
Если же f(a)* f(x1)>0 или f(b)* f(x1)<0, то новая область изоляции корня – [x1;b]. В этом случае второе приближение к корню
x2= 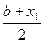 .
.
Теперь вычисляется f(x2) и снова определяется знак произведения f(x2)* f(x1), а по этому знаку определяется новая область изоляции корня. С каждым таким шагом эта область сужается, а значит, все точнее определяется значение корня уравнения. Процесс приближения заканчивается, когда выполняется одно из неравенств:
 (1)
(1)
или 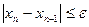 , (2)
, (2)
где  и
и  - допустимые погрешности определения корня.
- допустимые погрешности определения корня.
Дата добавления: 2015-10-13; просмотров: 77 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Облако в штанах | | | Метод хорд |