Метод хорд

По методу хорд точки, соответствующие значениям функции f(x), соединяются отрезком прямой, а за приблизительное значение корня уравнения f(x)=0 принимается точка пересечения этого отрезка с осью абсцисс. Затем вычисляется значение функции в этой точке и проводится новая хорда через эту точку и одну из точек на краю начальной области изоляции корня. Новое пересечение с осью абсцисс даст следующее приближение корня изоляции.

Порядок вычислений следующий: для начальной области корня [a;b] рассчитываем значения функции f(x) в точках ‘a’ и ‘b’, т.е. f(a) и f(b), а также значения вторых производных этой функции в этих же точках, т.е. f”(a) и f”(b). Затем определяется опорный край интервала, через который будут проходить все вычисляемые хорды:

X=a, если f(a)*f”(a)<0 или f(b)*f”(b)>0; (3)

X=b, если f(b)*f”(b)<0 или f(a)*f”(a)>0. (4)

Каждое приближение корня найдется по итерационной формуле:

x_n= x_n-1 - 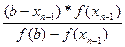, если Х=а;

x_n= x_n-1 - , если Х=b;

здесь х₀=Х.

Окончание итерационных вычислений определяется также по формулам (1) или (2).

Как следует из формул (3) и (4), необходимо определить вторую производную функции f”(x) или каким-либо другим способом правильно выбрать опорный край интервала изоляции корня, что может представлять определенные трудности. Еще одним недостатком метода является неудовлетворительный признак для завершения процесса итерационных вычислений, т.к. в некоторых случаях при выполнении условий (1) и (2) корень уравнения будет отличаться от х_n больше, чем на . Достоинством метода является меньшее, чем в методе дихотомии, число шагов вычислений при одинаковой погрешности нахождения корня.

Метод касательных

В этом методе, как в методе хорд, проводится прямая, а по точке пересечения ее с осью абсцисс находится приближенное значение корня уравнения. Отличие в том, что прямая проводится в виде касательной к функции в точке, принимаемой за предыдущее приближение корня.

Порядок вычислений следующий: сначала задается начальное приближение х=Х, где

Х=а, если f(a)*f”(a)>0 или f(b)*f”(b)<0;

X=b, если f(b)*f”(b)>0 или f(a)*f”(a)<0;

Затем по рекуррентной формуле определяем последующие приближения:

x_n=x_n-1 - ,

где (x_n-1) – производная функции f(x) в точке x_n-1.

Окончание вычислений производится по выполнению условий (1) или (2).

Метод обеспечивает нахождение корня с заданной точностью за небольшое число шагов приближений. Недостатки метода: если исходная функция не имеет первой производной, то метод невозможно применить; для расчетов и выбора начального приближения нужно вычислить первую и вторую производную функции; для некоторых функций выполнение условий (1) или (2) не обеспечит определение корня с необходимой точностью.

Последний отмеченный недостаток метода одновременно справедлив и для метода хорд. Однако, приближения, найденные методам хорд и касательных, лежат с разных сторон от точного значения корня. Поэтому существенно улучшить точность вычисления корня можно, если воспользоваться обоими упомянутыми методами, а за конечное значение корня принять среднеарифметическое из

n -ых приближений, найденных по каждому методу.

Дата добавления: 2015-10-13