Метод итераций

В этом методе начальное уравнение f(x)=0 преобразуется к виду x= . В качестве начального приближения берется произвольное значение х_о из области изоляции корня [a;b]. Вычисляется первое приближение x₁= , затем второе - x₂= , …, x_n= . Такая итерационная последовательность сходится, приближаясь к точному значению корня, если

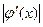<1 (5)

для любого х из области изоляции корня [a;b]. Если же условие (5) не выполняется, то для обеспечения сходимости итерационного процесса можно применить один из следующих способов дополнительных преобразований: изменение вида уравнения, переход к обратной функции, подбор множителя. Ознакомиться с этими способами можно, например в[1,2].

Итерационные вычисления заканчиваются при достижении условия .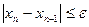

Решение алгебраических и трансцендентных уравнений в среде MATLAB

Решение уравнений на компьютере возможно при использовании большого числа популярных математических пакетов (сред), например: Derive, Mathcad, Maple, Matlab, Mathematica и другие. В данной лабораторной работе осваиваются некоторые средства численного и символьного способов решения линейных и нелинейных уравнений, представленные в среде Matlab.

Вещественные корни уравнений, представленных в виде f(x)=0, могут быть найдены с помощью команды fzero(param). Набор параметров команды может включать несколько элементов, разделяемых запятыми. Минимальный набор состоит из символической записи уравнения, точнее - его левой части, и скаляра или вектора, задающего начальное приближение для корня уравнения. Например: для уравнения 2х²+3-е^х=0 с помощью построения графика

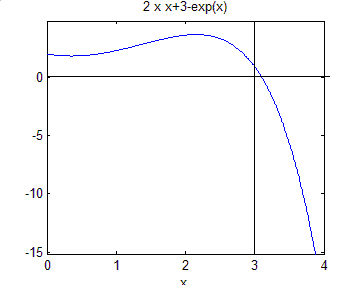
определяем область изоляции корня [3; 3,5]. Теперь вводим в командную строку

>> f='2*x*x+3-exp(x)'; x0=fzero(f,3.4) (6)

или

>> f='2*x*x+3-exp(x)'; x0=fzero(f,[3,3.5]) (7)

и получаем значение корня уравнения

x0 =

3.1022

В первом варианте – запись (6) – введено приближенное значение корня, оцененное из графика; во втором варианте – запись (7) – введен интервал значений для области изоляции корня. Результат получен один и тот же. Если уравнение имеет несколько вещественных корней, то команду fzero(param) вводят для каждой области изоляции корня.

Дополнительные параметры, которые могут быть заданы в команде fzero(param), это заданная погрешность вычисления корня и/или число допустимых при расчетах итераций. Например, если для выше рассмотренного уравнения задать допустимую погрешность 10^-7, а максимальное число итераций 20, то решение примет вид

>> f='2*x*x+3-exp(x)'; x0=fzero(f,[3,3.5], 1e-007, 20)

Func-count x f(x) Procedure

1 3 0.914463 initial

2 3.5 -5.61545 initial

3 3.07002 0.307702 interpolation

4 3.10369 -0.014187 interpolation

5 3.1022 0.000430236 interpolation

6 3.10225 5.74132e-007 interpolation

7 3.10225 -5.53039e-006 interpolation

Zero found in the interval: [3, 3.5].

x0 =

3.10224559385398

Чтобы показать, что Matlab использует разные методы численного решения уравнений в зависимости от начальных условий, решим рассматриваемое уравнение еще раз:

>> f='2*x*x+3-exp(x)'; x0=fzero(f,3.4, 1e-007, 20)

Func-count x f(x) Procedure

1 3.4 -3.8441 initial

2 3.30383 -2.38614 search

3 3.49617 -5.54239 search

4 3.264 -1.84655 search

5 3.536 -6.32273 search

6 3.20767 -1.14309 search

7 3.59233 -7.509 search

8 3.128 -0.259509 search

9 3.672 -9.36332 search

10 3.01533 0.788577 search

Looking for a zero in the interval [3.0153, 3.672]

11 3.06634 0.341658 interpolation

12 3.10396 -0.0169336 interpolation

13 3.10219 0.000573018 interpolation

14 3.10225 9.12357e-007 interpolation

15 3.10225 -5.19217e-006 interpolation

Zero found in the interval: [3.0153, 3.672].

x0 =

3.10224555947761

Изменился не только результат (при той же погрешности), но и число потребовавшихся итераций возросло, причем после десятого шага итераций поменялся и метод нахождения корня.

Matlab обладает также средствами символьного решения уравнений. В частности, команда solve(param) может находить корни уравнения, даже если все коэффициенты или их часть заданы не числами, а буквенными символами. Синтаксис команды таков:

>> solve('f(x)',x),

где 'f(x)' – записанное в символьном виде (в одиночных кавычках) решаемое уравнение;

х - переменная, относительно которой надо решить уравнение. Причем, если эта переменная обозначена как «х», то ее указывать не надо.

Для демонстрации использования команды solve(param) приведем два примера:

1. 3x⁵-9х+1=0 =>

>> y=solve('3*x^5-9*x+1=0')

y =

[ -1.3424984961381329368416258501782]

[ -.27655422116321279186867277544402e-1-1.3175273419010982681157610007208*i]

[ -.27655422116321279186867277544402e-1+1.3175273419010982681157610007208*i]

[.11111675757487677259648163090340]

[ 1.2866925827958987226188787743636]

Получили пять корней, два из которых комплексные, а три вещественных. Команда fzero(param) не нашла бы комплексные значения.

2. e^-2x – 5a =0 =>

>> y=solve('exp(-2*x)-5*a=0')

y =

-1/2*log(5*a)

Найден вещественный корень x₁=- , а комплексные утеряны. Иногда команда solve(param), наоборот, находит только комплексные корни, теряя вещественные. Как видим, в параметрах этой команды нет области изоляции корня. Это упрощает решение, но, возможно, служит причиной потери части корней.

Еще одна команда в среде Matlab предназначена для нахождения корней степенных полиномов – roots(A), где A – вектор коэффициентов полинома, выстроенных по порядку: сначала коэффициент при старшей степени переменной, затем – при степени на единицу меньшей и т.д. вплоть до свободного члена. Отсутствующие степени имеют нулевые коэффициенты, их обязательно включать в вектор.

Пример: степенной полином 3х⁶-7х⁴+9х-3 имеет вектор коэффициентов A =[3,0,-7,0,0,9,-3]. Поэтому корни полинома найдутся так:

>> A=[3 0 -7 0 0 9 -3]; z=roots(A)

z =

-1.73666998649015

-0.50372557202549 + 0.92130851107221i

-0.50372557202549 - 0.92130851107221i

1.20024597497171 + 0.28149418165882i

1.20024597497171 - 0.28149418165882i

0.34362918059771

Отметим, что в команде roots(A) коэффициенты могут быть заданы только числами.

Для закрепления изученного материала необходимо решить следующие уравнения и найти корни полиномов:

1. 36x - 3^x = 0 (-1,5) 0.0287 4.66

2. e^-5x –5/x + 25 = 0 (-1,1) 0.197

3. x² – ln(9 – 4x) = 0 (-2,2) 1.98 -1.66

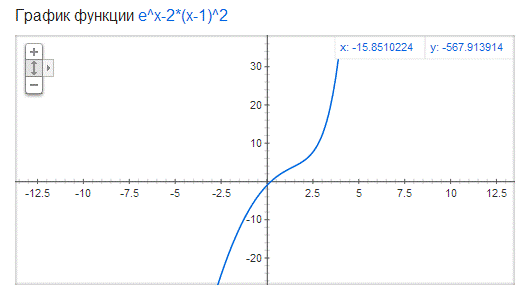
4. e^x – 2(x – 1)² = 0 (-0.5, 0.5) 0.2132

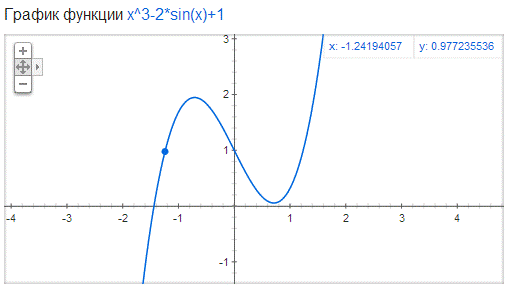
5. x³ – 2sin x + 1 = 0 (-2,2) -1.439

6. 5sin(ln x) + 1 = 0 (0, 30) 0 0,817 28,3

7. e^-ax + e^ax – ln a = 0

8. a(sin x + b) – ln(x + b) = 0

9. 3c – 2 ln(cos x) = 0 (8)

10. x⁸ – x⁷ + x⁶ – x⁵ + x⁴ – x³ + x² –x + 1 = 0

11. x¹¹ + x⁶ + x + 2 = 0

12. x⁵ – 5 = 0

Порядок выполнения заданий

1. Изучить теоретический материал работы.

2. Решить в среде Matlab двенадцать тренировочных уравнений (8): с первого по шестое командами fzero() и solve(), уравнения с седьмого по девятое - командой solve(), с десятого по двенадцатое - roots(). Проанализировать полученные результаты.

3. Предоставить преподавателю результаты п.2 и получить контрольное индивидуальное задание.

4. Результаты индивидуального задания представить в распечатанном виде.

Контрольные вопросы

1. В чем заключается метод дихотомии?

2. Каков алгоритм нахождения корня уравнения по методу хорд?

3. Каков алгоритм нахождения корня уравнения по методу касательных?

4. Сравнить между собой методы дихотомии, хорд и касательных.

5. Каков алгоритм нахождения корня уравнения по методу итераций?

6. Какие команды среды Matlab предназначены для нахождения корня уравнения?

7. Какова область применения команды fzero()?

8. Какова область применения команды solve()?

9. Какова область применения команды roots()?

10. Как задать параметры для команды fzero()?

11. Как задать параметры для команды solve()?

12. Как задать параметры для команды roots()?

Список литературы

1. Половко А.М., Бутусов П.Н. MATLAB для студента. – СПб.: БХВ-Петербург, 2005. – 320 с.: ил.

2. Половко А.М., Ганичев И.В. Mathcad для студента. - СПб.: БХВ-Петербург, 2006. – 336 с.: ил.

3. Hunt, Brien R Matlab R2007 с нуля! Книга + Видеокурс.: [пер. с англ.]/Brien R. Hunt [и др.]. – М.: Лучшие книги, 2008. – 352 с.: ил. + CD-ROM.

Дата добавления: 2015-10-13