Алгоритм Дейкстры

Результатом алгоритма поиска кратчайшего пути является последовательность ребер, соединяющая заданные две вершины и имеющая наименьшую длину среди всех таких последовательностей.

Жадный алгоритм построения минимального остовного дерева непригоден для поиска кратчайшего пути между двумя вершинами, поскольку на каждом проходе он учитывает длину лишь одного ребра.

Если же изменить его так, чтобы при выборе ребра, ведущего в кайму, он выбирал ребро, являющееся частью кратчайшего в целом пути из начальной вершины, то мы получим требуемый результат. Точнее говоря, вот измененный алгоритм:

Шаг 1. Выбрать начальную вершину

Шаг 2. Создать начальную кайму из вершин, соединенных с начальной

Шаг 3. Вершина назначения не достигнута?

Если нет, то переход на Шаг 4.

Иначе – переход на Шаг 9

Шаг 4. Выбрать вершину каймы с кратчайшим расстоянием до начальной

Шаг 5. Добавить эту вершину и ведущее в нее ребро к дереву

Шаг 6. Изменить кайму путем добавления к ней вершин, соединенных с вновь добавленной

Шаг 7. Для всякой вершины каймы выполнить: приписать к ней ребро, соединяющее ее с деревом и завершающее кратчайший путь к начальной вершине

Шаг 8. Переход на Шаг 3

Шаг 9. Конец

Проиллюстрируем алгоритм на примере графа, приведенного на Рис. 3.6. Будем искать кратчайший путь от вершины A к вершине G.

Рис. 3.15. Начальная вершина

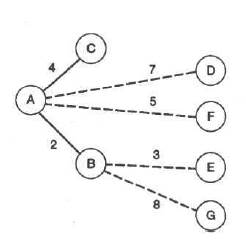
Рис. 3.16. Добавление второй и третьей вершин

Рис. 3.17. Добавление четвертой и пятой вершин

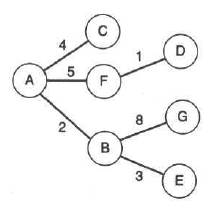
Рис. 3.18. Заключительные шаги алгоритма Дейкстры

Дата добавления: 2015-10-13